Linear Decision Treeと呼ばれる計算モデルについて解説します.
1. 決定木 (Decision Tree)
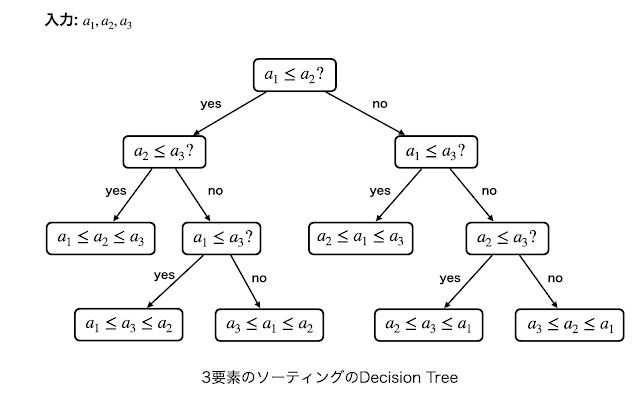
「ソートアルゴリズムは$\Omega(n\log n)$時間かかる」という話をよく聞くと思いますが, これは「ソートアルゴリズムは2要素の比較を$\Omega(n\log n)$回しなければならない」ことを意味します. 具体的には各ノードに「$a_i\leq a_j$?」と書かれた二分木があり, YESならば右の子ノード, NOならば左の子ノードに辿っていき葉に至ったらそこで終了しそこに書かれているラベル (例えば「$a_3\leq a_1 \leq a_2 \leq a_4$」のような要素の順位が書かれている)を出力するという計算モデルを考えています. このように二分木にYES/NOの質問が書かれており, その答えに対応する子ノードを辿っていき葉に至ったら終了するという計算モデルを決定木 (decision tree) といいます.
例えば上記の決定木では, どんな入力が与えられても質問に3回答えれば葉に至ります. このように. 決定木の効率性は主にその深さによって測ります (もちろん全体のノード数が小さい方が良いですが). ここで, 深さ$D$の決定木の葉の個数は$2^D$くらいです. つまり深さ$D$の決定木は高々$2^D$通りの出力しか区別することができないので, 出力しうるラベルの種類が$N$であるような問題を考えるとその問題を解く決定木の深さは$\lceil\log_2 N\rceil$必要であるという情報論的な下界が得られます. 例えば$n$要素のソートでは$n!= 2^{\Theta(n\log_2 n)}$通りのラベルを区別しなければならないため深さは$D=\Omega(n\log n)$となります. ある問題に対してその問題を解く決定木の深さの最小値を決定木複雑性 (decision tree complexity) といいます. ソートの決定木複雑性は$\Omega(n\log n)$ですが, 実際にマージソートなどは高々$O(n\log n)$回の数値比較でソートをするので, この下界は定数倍を除いてタイトとなります.
決定木の深さはちょうどクエリに回答する回数に対応するため, 計算時間に対応していると解釈できるわけです.
2. 線形決定木
一般に決定木のノードに書かれるラベルはどんな質問でも構いません. 極端な例で言うとノードのラベルにSATのインスタンスが書いてあってそれがYESインスタンスならば左の子に, そうでなければ右の子に辿るようなものを考えてもよいです. しかしながらそれでもなおソートの決定木複雑性は$\Omega(n\log n)$になります.
決定木のノードラベルの質問を線形不等式「$c_1a_1+c_2a_2+\dots+c_na_n\geq 0?$」の形に制限したものを線形決定木 (linear decision tree) といいます. ここで$a_1,\dots,a_n$は入力, $c_1,\dots,c_n$は適当な定数とします. また, 全てのノードのラベルにおける係数に含まれる非ゼロ要素が高々$k$個であるとき, 特に$k$-線形決定木 ($k$-LDT) といいます. 例えばソートの二要素の比較は$a_i-a_j\geq 0$と書き換えることができるので2-LDTとなります.
幾何的な解釈としては, 入力全体の空間を超平面で分割 (線形不等式クエリに対するYES/NOの応答に対応)していき「ラベル1を出力すべき入力の全体」「ラベル2を出力すべき入力の全体」...を区別していくことになります.
3. 決定木とアルゴリズムの違い: uniform vs nonuniform
一つの決定木は固定サイズの問題しか解くことができません. 従って決定木を使って問題を解く場合は決定木の族$(\mathcal{T}_n)_{n\in\mathbb{N}}$を考えます. 問題Pのサイズ$n$の任意の入力$x$に対し, $x$の答えを$\mathcal{T}_n$を使って計算できる時に$(\mathcal{T}_n)$は問題Pを解くといいます. つまり, 与えられる問題のサイズに応じて異なる決定木を使って良いということになります.
一方でアルゴリズムを使って問題を解く時は入力サイズがどのような場合であっても必ず同一のアルゴリズムを使わなければなりません. このように, 決定木とアルゴリズム(正確にはチューリングマシン)の間には問題サイズによって異なるものを使って良いかどうかという重要な違いがあります. 決定木のように問題サイズごとに異なるものを使う計算モデルをnonuniform, チューリングマシンのようにどのような問題サイズであっても同じものを使う計算モデルをuniformといいます.
UniformとNonuniformな計算モデルのギャップは未解決な部分が多いですが, 少なくともギャップが存在することが分かっています. 具体的にはnonuniformな計算モデルを使うと停止性判定問題を解くことができます (以前の記事参照). ちなみにnonuniformな計算モデルの計算量として最もよく研究されているのは(私の主観ですが)回路計算量だと思います.
今回の記事では線形計算機とアルゴリズムのギャップを, 3SUMという問題に焦点を当てて見ていきます.
4. 3SUMのLDT複雑性
3SUMという問題は
$n$個の数字$A=\{a_1,\dots,a_n\}\in\mathbb{R}$が与えられた時に$a_i+a_j+a_k=0$となる$i,j,k$が存在するか?
を判定する問題です. $a_i+a_j$を格納したサイズ$n^2$の配列Xを用意してこれをソートした後, 各$a_k$に対して$X$が$-a_k$を含むかどうかを二分探索でチェックすれば$O(n^2\log n)$時間で解くことができます. また, 前回の記事で紹介したように$O(n^2)$時間アルゴリズムも存在します. しかしながら任意の定数$\epsilon>0$に対し$O(n^{2-\epsilon})$時間アルゴリズムが存在するかどうかは未解決で, 精緻な計算量 (fine-grained complexity)の分野では$n^{2-o(1)}$時間かかると予想されています. とりあえず詳しくない人は「3SUMを$n^{1.99999}$時間で解くアルゴリズムは知られていない」と思っておけば大丈夫です.
本記事では3SUMのLDT複雑性に関する以下の驚くべき結果の証明(概略)を説明します.
定理1 ([1])
3SUMを解く深さ$O(n^{1.5}\log n)$の4-LDTが存在する.
実は3SUMを解く任意の3-LDTは深さが$\Omega(n^2)$あることが知られていたため[2], 4-LDTにすると一気に深さが減らせるというのはLDT界隈の人にとっては驚くべき事実だったことは想像に難くありません. 何よりも「3SUMは$O(n^{1.5}\log n)$回の要素の比較で解ける」ということになるわけです.
しかし定理1の証明はかなり単純かつ非常に賢いアイデアに基づいています. 定理1の4-LDTは以下のステップからなります.
ステップ1. 入力$A=\{a_1,\dots,a_n\}$を昇順にソートする.
ステップ2. $A$の各要素を連続した$\sqrt{n}$個ずつに分割してそれらを$A_1,\dots,A_{\sqrt{n}}$とする.
ステップ3. $L:=\cup_{i\in[\sqrt{n}]}\{x-y\colon x,y\in A_i\}$をソートする.
ステップ4. 以下のしゃくとり法っぽい計算を行う. ただし文中に出てくる$A_{st}$は$A_{st}:= \{x+y\colon x\in A_s,y\in A_t\}$とする.
for a in A:
$s \leftarrow 0$
$t \leftarrow \sqrt{n}$
while $s\leq t$:
if $-a\in A_{st}$ then: (1)
return True
elif $-a > \max(A_s)+\min(A_t)$: (2)
$s\leftarrow s+1$
else: (3)
$t\leftarrow t-1$
return False
正当性 (イメージ).
(1)において$-a\in A_{st}$となるならば, ある$b\in A_s,c\in A_t$に対して$-a=b+c$, すなわち$a+b+c=0$となるので, 確かにYESインスタンスとなります. 逆に, 入力がYESインスタンスであるとします. このときwhile文以下のループ処理は以下のような幾何的な解釈ができます:
入力$A=\{a_1,\dots,a_n\}$に対し, 点集合$P=\{(a_i,a_j):a_i,a_j\in A\}$を$xy$平面にプロットする. 各$a\in A$に対して直線$x+y=-a$上に乗っているような$P$の点の有無を判定していきます. ここで, $\mathbb{R}^2$を図のよう長方形で区切っていき, 各グリッドが$P$の点を$n$個ずつ含むようにします (実際には図のようなグリッドにはならないとは思いますが, 説明の簡単のためグリッドで区切っています). すると, while文の最初の時点では$s=0,t=\sqrt{n}$で点$(b,c)\in A_s\times A_t$に着目するわけですが, これは最も左上にある長方形に着目することに対応します. (1)では着目している短形内に直線上の点があるかどうかを判定しています. (2)と(3)では短形内の右下にある点に着目し, この点と直線の位置関係によって右隣か下の短形どちらに進むべきかを判断しています.
3SUMのLDTのしゃくとり法のイメージ (右の吹き出しの$\sqrt{n}$はタイポで正しくは$n$です)
深さの解析.
- ステップ1はマージソートをそのまま実装すれば良く, 深さ$O(n\log n)$の2-LDTで実装できます.
- ステップ2は分割しただけです.
- ステップ3はステップ1と同様にソートするだけです. $L$の要素数は$n^{1.5}$なので, 深さは$O(n^{1.5}\log n)$となります. また, $L$の各要素は$a_i-a_j$の形で書けるため, 4-LDTとなります.
- ステップ4では, while文が$s\leq t$である限り続けますが1回の反復で$t-s$は1ずつ減少するため, 高々$\sqrt{n}$回の反復で終了します. 各反復では(1)の処理がボトルネックになります. もし各$A_{st}$があらかじめソートしてあるならば二分探索ができるので(1)は$O(\log n)$時間で行うことができます. しかしながら全ての$A_{st}$をソートしようとすると, $0\leq s\leq t\leq \sqrt{n}$に対し各$A_{st}$は要素数$n$を持つため, $O(n^2\log n)$時間または同程度の深さのLDTが必要になってしまいます.
ここで, ステップ3で$L$をソートしているという事実に着目しましょう. $L$の全ての要素の大小を比較しているため, 各$i,j$と$a_i,a'_i\in A_i$, $a_j,a'_j\in A_j$に対し
$$a_i-a'_i \leq a_j-a'_j$$
またはその逆方向の不等式どちらが成り立つかが分かっています. これを移項すると
$$a_i+a'_j \leq a'_i+a_j$$
となりますが, この両辺はともに$A_{ij}$の要素です. これら4つの要素は任意にとって良かったので,
$L$の大小関係の情報が確定すれば各$A_{ij}$の全ての2要素の大小関係の情報は必ず確定します.
決定木でステップ1,2,3を経たノードにいるならば, $L$の要素の大小の順位の情報が確定しているということになるわけなので, 必然的に全ての$A_{ij}$の大小関係の情報が確定しており, 実質的に全ての$A_{ij}$がソートされているとみなすことができます. そこでこの情報を使ってステップ4で二分探索を行うことができるので, 全体の深さは$O(n^{1.5}\log n)$となります.
5. 何が肝なのか?
4章で紹介したLDTでは, ステップ3で計算した$L$の大小関係を使ってステップ4(1)で行う二分探索のために必要な$A_{st}$の要素の大小関係の情報を得られる, という部分が本質的に最も効いています. あくまでも「得られる」というわけであって「簡単に計算できる」というわけではないのがミソです。例えばソートアルゴリズムをそのままLDTに翻訳した場合は「$a_i-a_j\geq 0?$」というノードに対してインデックス$i,j$を簡単に計算して求められていたのですが, 今回考えたLDTではこのようなインデックスは存在性が保証されているだけであって簡単に計算できるとは限らないという点がポイントです。このように存在性と計算可能性のギャップがチューリングマシンとnonuniformモデルのギャップに繋がってくるのは面白い観点だと思いました。
参考文献
[1] Allan Grønlund and Seth Pettie, Threesomes, Degenerates, and Love Triangles, JACM, 65(4), pp.1--25, 2018 (preliminary version is in FOCS14).
[2] Jeff Erickson, Bounds for linear satisfiability problems, Chicago J. Theor. Comput. Sci.,1999(8), 1999 (preliminary version is in SODA95).