私自身そこまで詳しくはなく, 考えていたら面白い解釈を思いついたので記事に起こした次第です.
形がシンプルで, よく考えると劣モジュラ性に現れる限界効用逓減性っぽい雰囲気が感じられ, さらに名前がカッコイイので個人的に激アツな不等式です.
準備
・$\{0,1\}^m$上の離散確率を考える (例えばErdős–Rényi model).
・$f,g:\{0,1\}^m \to \mathbb{R}_{\geq 0}$ ... monotone increasing ($\{0,1\}^m$上の順序はbitwiseで比較)
・各$i=1,\ldots,m$に対してbinaryな確率変数$X_i$を定め, $\Pr(X_i=1)=p_i$とする.
・このとき, $f(X_1,\ldots,X_m)$ と $g(X_1,\ldots,X_m)$ は確率変数となる.
定理 (FKG不等式)
$\mathrm{E}[fg]\geq \mathrm{E}[f]\mathrm{E}[g]$.
実は$\{0,1\}^m$は束にまで一般化できる.
Remark.
・$f,g$がどちらも monotone decreasing でも成り立ちます (両辺に $-f,-g$ を代入).
・要するに共分散 $\mathrm{Cov}[fg]\geq 0$ と言っているだけなので, 両方ともmonotone ならば正の相関がある, みたいな認識です.
例 (Erdős–Rényi modelの部分グラフ)
$f,g$としてindicator functionを考えるのが一番簡単でしょう.
$m=\binom{n}{2}$, $p_i=p\in[0,1]$とすると, この設定はErdős–Rényi model $G(n,p)$と同等になる. その頂点集合を$V=[n]=\{1,\ldots,n\}$と定め, $Z_1,\ldots,Z_k\subseteq E(K_n)$を$V$上の完全グラフ$K_n$の辺部分集合とする.
例えば, 二頂点$s,t\in V$を固定し$Z_1,\ldots,Z_k$を$st$を結ぶ長さ4のパスの全体を考えたりできます. ここで各$Z_i$は頂点にラベルがついていることに注意してください. 従ってこの例だと$k=(n-2)(n-3)(n-4)$となります.
ここで確率
$\Pr(\forall i,Z_i\not\subseteq G(n,p))$
を考えます. FKG不等式を用いると
$\Pr(\forall i,Z_i\not\subseteq G(n,p))\geq \prod_i \Pr(Z_i\not\subseteq G(n,p))$
が簡単に示せます (実は使わなくても簡単に示せますが...). それを確認してみましょう.
もし,
が成り立つとしましょう (この部分をFKG不等式を使って示します).
すると
となり, 帰納的に
となります. 最後に成り立つと仮定した部分ですが,
とおくと, monotone increasing (言い換えれば$f(G+e)\geq f(G)$ for any $e\in \binom{V}{2}\setminus E(G)$) なので, FKG不等式より
$\mathrm{E}[fg]\geq \mathrm{E}[f]\mathrm{E}[g]$.
上式にある$\mathrm{E}(\cdot)$はそれぞれindicatorの期待値なので対応する確率となる (証明終).
限界効用逓減性
上の例では$f,g$を事象のindicatorとしていました. それに倣い, $f,g$をそれぞれ事象$A,B$のindicatorとしましょう. FKG不等式より
$\Pr(A\cap B)=\mathrm{E}[fg]\geq \mathrm{E}[f]\mathrm{E}[g]=\Pr(A)\Pr(B)$.
言い換えれば $\Pr(A|B)\geq \Pr(A)$ となります. これを情報量の言葉で書き換えると
$-\log \Pr(A|B) \leq -\log \Pr(A)$ です. つまり「Bの発生を知った上でのA発生の情報量」は「A発生の情報量」より少ないことを意味します. 解釈として, 例えば「食べログで高評価(=Bで条件付けられている)の店Sに入って美味しいものを食べたときの感動(=Aの情報量)」は「なんとなく入った店Sで美味しいものを食べたときの感動」よりも相対的に小さいという感じです.
もちろんこの解釈は$f,g$をindicatorに限った時の話であって, FKG不等式はこれをより一般に単調関数について拡大した不等式である, という見方ができるんじゃないかと思います.
FKG不等式の応用先
- Jansonの不等式の証明
- 本記事で証明したrandom graphのsubgraphの話
- 乱択アルゴリズムの解析 (PPSZ algorithmなど)
など

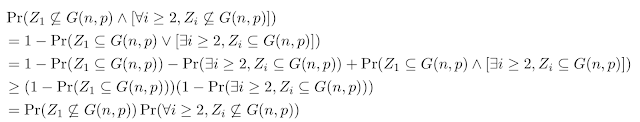




0 件のコメント:
コメントを投稿