1. 全点対最短経路問題
与えられたグラフ$G=(V,E)$の各頂点対に対してその間の最短経路長を求める問題を全点対最短経路問題 (APSP; All-Pairs Shortest Paths) といいます. この問題の計算量は入力のグラフが辺重みを持つかどうかで変わってくると信じられています.
この記事では$O(nm)$時間のアルゴリズムであっても計算量は$O(n^3)$と表記します (つまり$m$への依存は考慮せず, 最悪ケースの$m=n^2$だけを考える).
1.1. 辺重み有りの場合:
負閉路が存在しなければWarshall-Floyd法により$O(n^3)$時間で解くことができます. Warshall-Floyd法以外にも様々なアルゴリズムが提案されており, 以下の表のようななっています.
2021年12月現在ではWilliams(2014)による$n^3/\exp(\Omega(\sqrt{\log n}))$時間が(オーダーの意味で)最速ですが, $\exp(\sqrt{\log n})=n^{1/\sqrt{\log n}}=n^{o(1)}$なので, 任意の定数$\epsilon>0$に対して(重み付きグラフの)APSPを$O(n^{3-\epsilon})$時間で解くアルゴリズムは知られていません. つまり, およそ60年にわたってWarshall-Floyd法は$n^{o(1)}$倍の改善はあれど, $n^{\epsilon}$倍の改善はなされていません! このことから2010年代からは
任意の定数$\epsilon>0$に対して重み付きグラフのAPSPは$O(n^{3-\epsilon})$時間で解けない
という命題 (APSP予想と呼ばれる) が正しいという強い仮定の下で他の様々な問題の"精緻な"計算量下界が明らかにされてきました. これはちょうど, 「$\mathrm{P}\neq\mathrm{NP}$の下では最大カットは多項式時間で計算できない」などといったNP困難性の議論と同じ流れです (仮定する命題は大きく異なる). このアプローチは精緻な計算量 (fine-grained complexity) と呼ばれ, 以前の記事でも紹介しているので興味のある方は読んでみてください.
1.2. 辺重みなしの場合
辺重みなしグラフのAPSPは, 以前の記事で紹介したSeidelのアルゴリズムによって高速行列積に基づいた高速なアルゴリズムが知られており, 二つの$n\times n$行列の積の計算が$O(n^\omega)$時間でできるならば重みなしグラフのAPSPは$O(n^\omega\log n)$時間で計算できます. 2021年12月現在では$\omega < 2.37286$であることが知られています [Alman and Williams, 2021].
しかしながら, 高速行列積のアルゴリズムは複雑で, 実用上では素朴な$O(n^3)$時間アルゴリズムの方が高速であることが多いとされています. 従って高速行列積を使わない"組合せ的な"アルゴリズムの存在性が研究の議題になることもあります (e.g., [Bansal and Williams, 2012]).
2. 重みなしAPSPの近似アルゴリズム [DHZ00]
行列積が$O(n^2)$時間で計算できるならば重みなしグラフ上のAPSPも$O(n^2\log n)$時間で解けるのですが, 現状ではまだまだ程遠いです. 一方で行列積に基づかないAPSPアルゴリズムというのは自明な$O(n^3)$時間アルゴリズムとほぼ同程度の計算量しか達成されておらず, 例えば$O(n^{2.999})$時間のものは知られていません.
本記事では, 行列積を使わずにAPSPの(+2)近似を$O(n^{7/3}\log n)$時間で計算する乱択アルゴリズムを紹介します [Dor, Halperin, Zwick, 2000]. ここで, APSPの(+2)近似は全ての頂点対$u,v$に対して, $uv$間の最短経路長を$d(u,v)$と表すとして, $d(u,v)\leq D(u,v) \leq d(u,v)+2$を満たす$D(u,v)$を計算することを意味します. また, このアルゴリズムはランダムシードに依らず必ず$O(n^{7/3}\log n)$時間で終了しますが高確率(確率$1-O(1/n)$)で(+2)近似を計算します.
一般に近似精度が理論保証されている近似アルゴリズムというのはNP困難な問題に対して最適値の$c$倍以内の解を出力する (つまり, 近似比の保証がある) 多項式時間アルゴリズムを指すことが多いですが, この記事では$n^3$時間で解ける問題に対してadditive errorの保証がなされている近似アルゴリズムを考えているのに注意してください.
なお, $7/3\approx 2.333... < \omega$ なので, 現在知られている高速行列積アルゴリズムよりも高速な近似アルゴリズムになっています. ちなみに論文のタイトルは All Pairs Almost Shortest Paths というオシャレなタイトルで, 著者の1人であるUri Zwickはcolor codingの元論文の著者の1人です. なお, APSPの(+2)近似を$O(n^2)$時間で計算するアルゴリズムなどは分かってないです.
まず, 頂点集合を次数の大きさによって以下の三つの部分集合に分割します:
$L=\{v\in V\colon \deg(v)<n^{1/3}\}$
$M=\{v\in V\colon n^{1/3}\leq \deg(v)\leq n^{2/3}\}$
$H=\{v\in V\colon \deg(v)>n^{2/3}\}$
($L,M,H$はそれぞれlow, medium, high degreeだと思ってください). 各最短経路を
- $L$内の頂点のみからなる最短経路
- $H$の頂点を少なくとも一つ含む最短経路
- $H$の頂点は一つも含まないが, $M$の頂点を少なくとも一つ含む最短経路
の三ケースに分けて考察します (下図).
2.1. $L$内の最短経路の計算
端点も含め全ての頂点が$L$に含まれるような最短経路を考えます. この最短経路は誘導部分グラフ$G[L]$に含まれるので, $G[L]$内で全頂点からBFSを行うことにより計算できます. このようにして得られた距離を$d_1(\cdot,\cdot)$とします (つまり, $u,v\in L$に対し$d_1(u,v)$は$G[L]$上の$uv$最短経路長).
$G[L]$に含まれる辺の本数は, $L$の次数制約より$O(n\cdot n^{1/3})$なので, このBFSは全体で$O(n^{7/3})$時間で完了します.
2.2. ランダムサンプリングによるHitting Setの計算
二つ目のケースを考える準備として, 別の記事で紹介したhitting setの概念を導入します. 頂点$v\in V$の隣接点の集合を$N(v)$と表すことにします. 頂点部分集合族$\{N(v)\colon v\in H\}$と$\{N(w)\colon w\in M\}$のhitting setをそれぞれ$S$と$T$で表します. 即ち,
$S$は$S\cap N(v)\neq \emptyset$ ($\forall v\in H$)
$T$は$T\cap N(w)\neq\emptyset$ ($\forall w\in M$)
をそれぞれ満たします. $S$は以下のような簡単なランダムサンプリングで計算できます:
$S=\emptyset$からスタートし, 各頂点$u\in V$に対して独立に確率$p:=2n^{-2/3}\log n$で$u$を$S$に追加する.
$H$に属する各頂点$v$は$\deg(v)\geq n^{2/3}$を満たすので, $N(v)$が一つも$S$に追加されない確率を考えると
$$\Pr[N(v)\cap S=\emptyset] \leq (1-p)^{n^{2/3}}\leq \exp(-n^{2/3}p) \leq n^{-2}.$$
よってunion boundより, $\Pr[\exists v\colon N(v)\cap S=\emptyset]\leq n^{-1}$, つまり$S$は確率$1-n^{-1}$で hitting set になる. さらに, $|S|$は独立な確率確率変数(indicator)の和になるので, Chernoff boundにより, 確率$1-n^{-1}$で$|S|=\mathbf{E}[|S|]=\Theta(n^{1/3}\log n)$を満たします.
同様のランダムサンプリングにより, $T$はサイズ$\Theta(n^{2/3}\log n)$を満たすようにとることが高確率でできます.
2.3. $H$を通過する最短経路の近似
先ほど計算したhitting set $S$の各頂点$s\in S$に対し, $s$を始点としたBFSを計算することによって, $\{d(s,w)\colon s\in S,w\in V\}$を$O(|S|n^2)=O(n^{7/3}\log n)$時間で計算できます. ここで, 全ての頂点$u,v\in V$に対して $d_2(u,v)=\min_{s\in S}\{d(u,s)+d(s,v)\}$ とします.
補題1.
$uv$間の最短経路であって$H$の頂点を含むものが存在するならば, $d(u,v)\leq d_2(u,v)\leq d(u,v)+2$.
(証明).
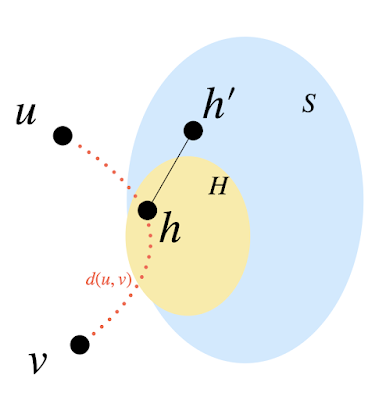
$h\in H$を通る$uv$最短経路を$P$とする. $S$はhitting setなので, $S\cap N(h)\in h'$とする(下図参照). このとき, 三角不等式より
$$d(u,v)\leq d_2(u,v)\leq d(u,h')+d(h',v)\leq d(u,h)+d(h,v)+2 =d(u,v)+2.$$
2.4. $H$を通らないが$M$を通る最短経路の近似 (方針)
このパートでは方向性だけ説明します.
$H$を通る最短経路は2.3で計算済みなので, 残りの最短経路は与えられたグラフから$H$を全て削除しても影響がありません. 残った辺は$L\cup M$に接続しており, $L\cup M$に属する頂点の次数は全て$\leq n^{2/3}$なので, 残った辺は$O(n\cdot n^{2/3})$本しかありません. つまりこのグラフはある程度は疎です!
残ったグラフ上で2.2で計算したhitting set $T$に属する各頂点$t$に対し, $t$を始点としたBFSを行い, $\{d_{G'}(t,v)\colon t\in T,v\in V\}$ を$O(|T|n^{5/3})=O(n^{7/3}\log n)$時間で計算します. ここで$d_{G'}(\cdot,\cdot)$は$G'$上の最短経路を意味します.
各頂点$u,v$に対し, $\min_{t\in T}\{d_{G'}(u,t)+d_{G'}(t,v)\}$を考えます. 補題1と同様の議論及び本パート冒頭の議論 ($H$間の辺の削除をしても, $H$を通過しない最短経路に影響はない) より, 以下が成り立ちます.
補題2.
元のグラフ上において, $uv$間の最短経路が$H$を通らないが$M$を通るとする. このとき, $d(u,v)\leq \min_{t\in T}\{d_{G'}(u,t)+d_{G'}(t,v)\}\leq d(u,v)+2$.
(図による証明)
残念ながら, $\min_{t\in T}\{d_{G'}(u,t)+d_{G'}(t,v)\}$を愚直に計算すると$O(n^2|T|)=O(n^{8/3})$時間かかってしまいます. 以下では別のグラフを新たに構成することによってこの計算を工夫します.
2.5. $d_3(u,v)$の計算アルゴリズム
各頂点$x\in V$に対し, 辺重みつきグラフ$G_x=(V,E_x)$を以下のように構成します: $E_x=\emptyset$から始めます.
- $L$に接続する辺を全て$E_x$に追加します. これらの重みは全て1とします. ここで追加される辺数は$L$の次数の条件より$O(n\cdot n^{1/3})$です.
- 各$t\in T$に対して$E_x$に辺$\{x,t\}$を追加します. この辺の重みを$d_{G'}(x,t)$とします. これらの重みは2.4で計算済みです. ここで追加される辺数は$O(|T|)=O(n^{2/3}\log n)$です.
- $T$-$M$間で元のグラフに含まれている辺を全て重み1の辺として$E_x$に追加する. すなわち, 各$m\in M$と全ての$z\in T\cap N(m)$に対し ($T$はhitting setなのでこのような$z$は必ず存在します), 重み1の辺$\{m,z\}$を$E_x$に追加する. ここで追加される辺数を考えて見ましょう. 各$t\in T$の次数は高々$n^{2/3}$ ($H$の頂点は削除したから) なので, 辺数は高々$$|T|\cdot n^{2/3}=O(n^{4/3}\log n)$です.
2.6. アルゴリズムの概要
2.1〜2.5で計算した三つの距離$d_1,d_2,d_3$に対し, $\min\{d_1(u,v),d_2(u,v),d_3(u,v)\}$を出力します. $d_3$は必ずしも対称性 ($d_3(u,v)=d_3(v,u)$) が成り立つとは限らないので, 対称性を保証するために$d_3(u,v):=\min\{d_{G_u}(u,v),d_{G_v}(v,u)\}$を計算しても良いです. これまで議論してきたように, $d_1$から$d_3$は高々$O(n^{7/3}\log n)$時間で計算でき, しかも補題1~3により(+2)近似であることが保証されます.
3. 余談 (Spanner)
密な重みなしグラフ$G=(V,E)$が与えられた時, そのグラフの全域部分グラフ$S=(V,E_S)$のうち頂点間の距離をできるだけ保つようなものをspannerといいます. もう少しフォーマルな定義をいうと, 二つの正のパラメータ$\alpha,\beta$に対して以下の条件を満たすとき, 全域部分グラフ$S$は$G$の$(\alpha,\beta)$-spannerであるといいます.
なので, もし辺数$|E_S|=m_S$の$(\alpha,\beta)$-spannerが$T(n)$時間で計算することが出来るならば, APSPに対する$T(n)+O(nm_S)$時間近似アルゴリズムであって, multiplicative と additive の error がそれぞれ$\alpha,\beta$となるようなものを与えることができます. ちなみに$(1+1/k,0)$-spannerを$O(n^{1+1/k})$時間で計算するアルゴリズムが構成できます. 別の記事でも紹介したように, spannerは理論計算機科学でもかなり活発に研究されている分野で, 組合せ論におけるErdős Girth Conjectureと深いつながりがあります.
3. まとめ
重みなしグラフ上のAPSPに対して$O(n^{7/3}\log n)$時間の(+2)近似アルゴリズムを紹介しました. このアルゴリズムは現状の高速行列積よりもオーダー的に高速で, それほど複雑でもないため苦労せず実装できるものになっています.
アイデアとしては次数によって頂点集合を分割し, 高次数の頂点を経由する最短経路はhitting setを使って近似するというものになっています.
これら二つのアイデアはそれぞれ





0 件のコメント:
コメントを投稿