0. 概要
本記事では
- ランダムグラフ理論の動機と応用
- ランダムグラフ理論のさわり
- ランダムグラフの面白い定理
について書きます.
1. ランダムグラフ理論の動機と応用
ランダムグラフ理論の主な動機としては
- 「とある性質Pを満たすグラフが存在するか?」という問に対する肯定的な解決
- 現実のネットワークにおける様々な現象の理論的説明
歴史的には1が重要で、グラフ理論における有名問題「任意に大きい彩色数と内周(長さ最小の閉路)を持つグラフは存在するか?」をErdősらが解決した際に初めてランダムグラフを用いられました. ロジックとしては「性質Pを満たすグラフの存在性」という問に対し, Pr[ランダムに生成したグラフがPを満たす確率]$>0$であることを示すことにより, この問を肯定的に解決する, というものになります.
2は応用上重要だと思います. 現実世界のネットワーク(複雑ネットワーク)にはスモールワールド性, 高いクラスタ係数, 次数のベキ乗則といった様々な現象が観測されます. そこでWSモデル, BAモデルといった複雑ネットワークを模倣するランダムグラフのモデルを解析することによってこれらの現象の発生を理論的に説明出来るようになります.
また, ランダムグラフはグラフアルゴリズムのベンチマークとして用いられることがよくあります. しかしベンチマークとして用いる際, そのランダムグラフはどのような性質(高い確率で連結なのか, 直径が小さいかどうかなど)を持つかについて知っておかなければいけません. 例えば「小直径グラフに対してはたまたま速く動作してしまうアルゴリズム」のベンチマークとして「高い確率で小直径になってしまうランダムグラフ」を(小直径になるとは知らずに)ベンチマークとして用いて数値実験を行い「ランダムグラフで高速に動いたから大体のグラフでも動く」と結論づけてしまったら最悪です. このような事態を避けるためにも, ランダムグラフの性質についての知識や簡単な導出過程については知っておくべきでしょう.
2. ランダムグラフ理論のさわり
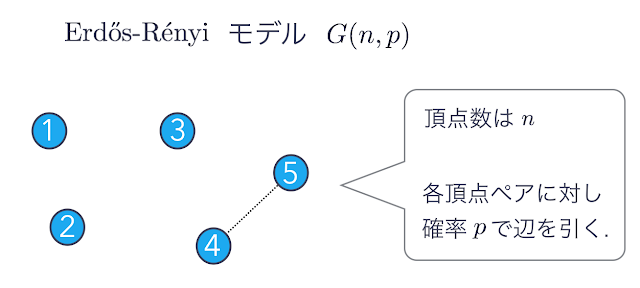
2.1. Erdos-Renyi (ER)モデル
頂点数 $n$ のグラフを考えます. 各頂点ペア $u \neq v$に対し, 確率$p$で独立に辺を引きます. このグラフ生成モデルを Erdos-Renyi(ER)モデルと呼び, 生成したグラフを$G(n,p)$で表します.
ERモデルはランダムグラフ理論で最も多くの研究結果があります. ERモデルは通常, パラメータ$p$を$p=p(n)$(つまり, $n$の関数)として, $n\to\infty$における$G(n,p)$の構造を解析します. グラフの性質$\mathcal{P}(例えば連結性, 平面性など)に対してPr[G(n,p)がPを満たす]$\to 1$ (as $n\to\infty$) ならば$G(n,p)$はほとんど確実に性質$\mathcal{P}$を満たすと言います. ランダムグラフ理論では$n$頂点のランダムグラフ(例えば$G(n,p)$)はどのような性質をほとんど確実に満たすのか, について解明している理論であると言い換えることも出来ます.
本稿では,
- $p=o(n^{-2})$(注*)ならば, $G(n,p)$はほとんど確実に辺を持たない.
- $p=\omega(n^{-2})$(注**)ならば, $G(n,p)$はほとんど確実に辺を持つ.
- $p\sim \alpha \cdot n^{-2}$(注***)ならば, $\mathrm{Pr}$[$G(n,p)$が辺を持つ]$\to 1-e^{\alpha/2}$.
を証明して, 最後に$G(n,p)$の他の面白い性質を簡単に紹介していくという流れになります.
(注*) $f,g:\mathbb{N} \to \mathbb{R}_{\geq 0}$に対し
$f(n)=o(g(n)) \, \iff \, \lim_{n\to\infty}\frac{f(n)}{g(n)}=0$
(注**) $f,g:\mathbb{N} \to \mathbb{R}_{\geq 0}$に対し
$f(n)=\omega(g(n)) \, \iff \, \lim_{n\to\infty}\frac{f(n)}{g(n)}=\infty$
(注***) $f,g:\mathbb{N} \to \mathbb{R}_{\geq 0}$に対し
$f(n)\sim g(n) \, \iff \, \lim_{n\to\infty}\frac{f(n)}{g(n)}=1 \,\iff\, f(n)=(1+o(1))g(n)$.
$f(n)\sim g(n) \, \iff \, \lim_{n\to\infty}\frac{f(n)}{g(n)}=1 \,\iff\, f(n)=(1+o(1))g(n)$.
2.2. First Order Method
$X$を非負の値をとる確率変数とします. 任意の$a>0$に対して

が成り立ちます. この不等式をMarkovの不等式と呼びます.
$G(n,p)$の辺数$m$は非負整数値をとる確率変数なので,
 .
.
$p=o(n^{-2})$ならば, $n^2p\to 0$ (as $n\to\infty$)より,
 .
.
以上より, $p=o(n^{-2})$ならば$G(n,p)$はほとんど確実に辺をもたないことが示されました. 他にも, $Y=G(n,p)$が含む三角形(長さ3の閉路)の個数 と定義すると,
$\mathrm{Pr}$($G(n,p)$が三角形を含む)$=\mathrm{Pr}(Y\geq 1) \leq \mathrm{E}[Y] \sim n^3p^3/6 \to 0$ (as $n\to\infty$).
となるので, $p=o(n^{-1})$ならば$G(n,p)$はほとんど確実に三角形を含まない ことが示せました. このように, Markovの不等式を用いて「ない」ことを示す証明技法をFirst Order Methodと呼びます. なぜ "First" なのかというと, 確率変数の一次モーメント(期待値)を計算するからです.
First Order MethodはMarkovの不等式を用いて「ない」ことを証明する技法でした. 一方でランダムグラフ理論では「ある」ことを証明する技法が知られています. それがSecond Order Methodです.
一般に, 平均と分散が有限となるような確率変数$X$に対してChebyshevの不等式と呼ばれる次の不等式が成り立ちます.
 .
.
ここで, $t=\mathrm{E}[X]$を代入すると,
したがって
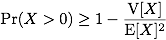 .
.
となります. この$X$が例えば「辺の本数」「三角形の個数」などを表すなら, この不等式は「辺が存在する確率」「三角形が存在する確率」の下界を与えることになります.
このように分散を使ってランダムグラフ内に「ある」ことを証明する技法を Second Order Method と呼びます. 分散$\mathrm{V}[X]$を計算するためには二次モーメント$\mathrm{E}[X^2]$を計算する必要があるため "Second" の名を冠しています.
また, $X$が非負整数値をとるとき, コーシーシュワルツの不等式を用いることで次のような不等式が示せます.



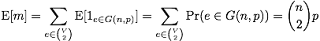

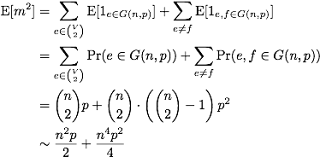
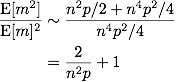
 .
.
三角形の個数も指示関数の和で表せるので, 全く同様にして同じようなことを示すことができ, 相転移を観察することが出来ます.
この節の最後に, monotonicity について紹介します. グラフの性質$\mathcal{P}$が以下の性質を満たすとき, $\mathcal{P}$はmonotone increasingであると言います.
「$G$が$\mathcal{P}$を満たすならば, $G$に任意の新しい辺$e$を追加して得られたグラフ$G\cup e$も$\mathcal{P}$を満たす.」
例えば, $\mathcal{P}$を「連結であるという性質」とします. $G$が$\mathcal{P}$を満たすとき, $G$は連結グラフです. そして$G$に新しい辺を追加しても連結なままです. 従って「連結性」は monotone increasing です. 他にも「辺を持つ」「直径$\leq 100$である」「辺連結度が100以上である」「ハミルトン閉路を持つ」などの数多くの重要な性質が monotone increasing となります.
一方、性質$\mathcal{P}$を満たすグラフ$G$からどの辺を削除しても依然として$\mathcal{P}$を満たすならば, 性質$\mathcal{P}$は monotone decreasing であるといいます. 例えば「平面的である」「森である」「ハミルトン閉路を持たない」などの性質が monotone decreasingとなります.
$\mathcal{P}$をmonotone increasingであるとします. このとき必ず相転移が発生するような閾値関数が存在するということが証明されています (Bollobas, Thomasson, 1997). 具体的には
nontrivial で monotone increasingな性質 $\mathcal{P}$に対し, ある$p^*=p^*(n)$が存在して
$p=\omega(p^*)$ならばほとんど確実に$G(n,p)$は$\mathcal{P}$を満たし, $p=o(p^*)$ならばほとんど確実に$G(n,p)$は$\mathcal{P}$を満たさない.
ことが示されています(monotone decreasing についても同様のことが成り立ちます). 例えば, 「辺を持つ」という性質では$p^*=n^{-2}$となります.
$p=o(n^{-2})$, $p=\omega(n^{-2})$に対する$G(n,p)$の辺の有無について解析してきました. それではこれらの中間, すなわち $p\sim c\cdot n^{-2}$のときはどうなるでしょうか?
$m$はiidな指示関数の和として書けるので, 二項分布$\mathrm{Bin}\left(\binom{n}{2}, p\right)$に従う確率変数です. ここで, ポアソンの極限定理によると,

となるので (ここでは確率密度関数が各点収束するという意), 今回の場合は
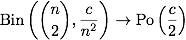
となります. 即ち, 辺の本数$m$は漸近的に平均$c/2$のポアソン分布に従うため, $\mathrm{Pr}(m=0) \to e^{- c/2}$ となります.
c/2}$ となります.
様々な性質$\mathcal{P}$について, $p$が閾値関数上のときの$G(n,p)$の振る舞いの確率にはポアソン分布が絡んできていることが分かっています. 例えば$G(n,p)$の頂点を一つ固定してその次数を確率分布 $d$ で表すと, 明らかに $d$ は二項分布 $\mathrm{Bin}(n-1,p) \sim \mathrm{Bin}(n,p)$に従います. 従って
・$p=o(n^{-1})$のときは

・$p=\omega(n^{-1})$のときは, $d$が指示関数の和で表せることを用いると

・$p\sim c\cdot n^{-1}$のときは, ポアソン極限定理より, $d$は漸近的に平均$c$のポアソン分布に従うため,

が簡単に示せます. 特に$d=0$ということは固定した頂点が孤立点であり, つまり$G(n,p)$が非連結であるということになるので,
 .
.
即ち $p\sim c/n$のときは正の確率で$G(n,p)$は非連結になることが示せました.
実際には頂点を$k$個だけ固定してそれぞれの次数を$d_1,\ldots,d_k$として$k$個の確率変数を定義すると, それぞれは漸近的に平均$c$のポアソン分布に従い, しかも実は漸近的にこれらの確率変数は独立であることが言えます. つまり
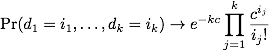
となり, グラフが連結であるならば $d_1>0,\ldots,d_k>0$となるので

今, $k$は任意の自然数だったので, 右辺は任意に小さくできるので,

つまり, $G(n,p)$はほとんど確実に非連結であることが示せました.
ランダムグラフ理論では閾値関数などの様々な定理が知られているので個人的に面白いと思ったものを列挙します.

とおきます. このとき

グラフ$G$が$k$-connectedであるとは, $G$を非連結にするためには最低でも$k$個の頂点を削除しなければならないことを意味します.

とします. このとき

ハミルトン閉路とは, 全ての頂点を一度ずつ通るような閉路のことです. 与えられたグラフがハミルトン閉路を持つかどうかを判定する問題はNP-完全で多項式時間では判定できないとされていますが, ランダムグラフがハミルトン閉路を含むかどうかもまた大きな難問でした.

とします. このとき,

グラフの独立点集合とは, 頂点部分集合$S\subseteq V$で$S$の任意の二頂点間に辺が存在しないようなものです. 独立点集合のうち要素数最大なものを最大独立点集合といい, その要素数を$\alpha(G)$と書きます. 与えられたグラフに対して$\alpha(G)$を計算する問題はNP-困難ですが, ランダムグラフ理論においては次の結果が知られています.
$p\in(0,1)$を定数とし, $b=\frac{1}{1-p}$とします. このときほとんど確実に

つまり, おおよそ $\alpha(G(n,p)) \simeq 2\log_b n$.
グラフの彩色(頂点彩色)とは, 頂点から色への写像で, 隣接頂点同士は異なる色に写される(塗られる)という性質を持ったものです. 彩色が存在するような色の種類数のうち最小の値を彩色数と呼び, $\chi(G)$で表します. 与えられたグラフ$G$に対して$\chi(G)$を計算する問題はNP-困難です.
$p\in(0,1)$を定数とし, $b=\frac{1}{1-p}$とします. すると
おおよそ $\chi(G(n,p)) \simeq \frac{n}{\log_b n}$ となります.
(注:) 彩色数と最大独立点集合の間には, $\chi(G)\alpha(G)\geq n$という関係があってこれを用いています.
ランダムグラフ理論の動機を概説し, first order method, second order ethod, Poisson approximation theoremについて紹介しました.
私は東大でランダムグラフ理論について研究していますが, 日本にはランダムグラフをやっている人があまり居ません(少し寂しいことですが...). ランダムグラフ理論で用いられる確率的議論(そしてそのアイデア)は, 乱択アルゴリズムの解析や組合せ論において非常に有用で, それらを学ぶことはランダムグラフのみならず他の分野でも大きな武器になるのではないかと思います(あと二項係数に強くなれます). グラフ理論と確率論のインターセクションにあるランダムグラフ理論はそれらの深い理解に通じる面白い理論であり, そしてランダムグラフ理論の勉強を通じて確率論の深い理解に繋がることがあるので, 本格的に研究しなくても学んでみる価値は大いにあると信じています.
[1] R. Diestel, "Graph Theory"
[2] A. Frieze, M. Karoński "Introduction to Random Graphs" (著者がドラフトをウェブ上で公開しています)
[3] Bollobás, "Random Graphs"
以上より, $p=o(n^{-2})$ならば$G(n,p)$はほとんど確実に辺をもたないことが示されました. 他にも, $Y=G(n,p)$が含む三角形(長さ3の閉路)の個数 と定義すると,
$\mathrm{Pr}$($G(n,p)$が三角形を含む)$=\mathrm{Pr}(Y\geq 1) \leq \mathrm{E}[Y] \sim n^3p^3/6 \to 0$ (as $n\to\infty$).
となるので, $p=o(n^{-1})$ならば$G(n,p)$はほとんど確実に三角形を含まない ことが示せました. このように, Markovの不等式を用いて「ない」ことを示す証明技法をFirst Order Methodと呼びます. なぜ "First" なのかというと, 確率変数の一次モーメント(期待値)を計算するからです.
2.3. Second Order Method
First Order MethodはMarkovの不等式を用いて「ない」ことを証明する技法でした. 一方でランダムグラフ理論では「ある」ことを証明する技法が知られています. それがSecond Order Methodです.
一般に, 平均と分散が有限となるような確率変数$X$に対してChebyshevの不等式と呼ばれる次の不等式が成り立ちます.
 .
.ここで, $t=\mathrm{E}[X]$を代入すると,
したがって
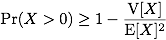 .
.となります. この$X$が例えば「辺の本数」「三角形の個数」などを表すなら, この不等式は「辺が存在する確率」「三角形が存在する確率」の下界を与えることになります.
このように分散を使ってランダムグラフ内に「ある」ことを証明する技法を Second Order Method と呼びます. 分散$\mathrm{V}[X]$を計算するためには二次モーメント$\mathrm{E}[X^2]$を計算する必要があるため "Second" の名を冠しています.
また, $X$が非負整数値をとるとき, コーシーシュワルツの不等式を用いることで次のような不等式が示せます.

これらの不等式から共通して言えることは, $\mathrm{E}[X^2]\sim \mathrm{E}[X]^2$が示せたら$\mathrm{Pr}(X>0)\to 1$が示せるということです.
それでは, $p=\omega(n^{-2})$として, $G(n,p)$が辺をほとんど確実に持つ, 即ち $\mathrm{Pr}(m>0)\to 1$ を示しましょう. ($m=m(G(n,p))$は$G(n,p)$に含まれる辺の個数を表す確率変数). 最も肝心なのは, $m$は指示関数の和で書き表わせるということです. 即ち, $n$頂点完全グラフ$K_n$の辺$e$に対して

という確率変数を定義したとき,

が明らかに成り立ちます. 従って, 期待値の線型性より
となり, 二次モーメント $\mathrm{E}[m^2]$については

となるので,
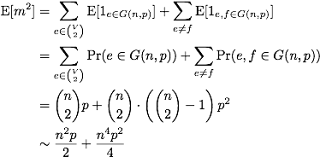
従って
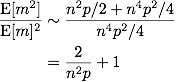
これを上記で紹介した不等式に代入すると, $p=\omega{n^{-2}}$より$n^2p\to \infty$なので,
 .
.
となって所望の命題が示せました. まとめると, $p=o(n^{-2})$ならば$G(n,p)$はほとんど確実に辺を持たないが, $p=\omega(n^{-2})$ならば$G(n,p)$はほとんど確実に辺を持つことが証明されました. このようにパラメータのオーダーを変えた瞬間に一気に性質のオンオフが変わってしまう性質のことを相転移(phase transition)と言います. ランダムグラフ理論ではこのような相転移現象が数多く証明されてます.
三角形の個数も指示関数の和で表せるので, 全く同様にして同じようなことを示すことができ, 相転移を観察することが出来ます.
この節の最後に, monotonicity について紹介します. グラフの性質$\mathcal{P}$が以下の性質を満たすとき, $\mathcal{P}$はmonotone increasingであると言います.
「$G$が$\mathcal{P}$を満たすならば, $G$に任意の新しい辺$e$を追加して得られたグラフ$G\cup e$も$\mathcal{P}$を満たす.」
例えば, $\mathcal{P}$を「連結であるという性質」とします. $G$が$\mathcal{P}$を満たすとき, $G$は連結グラフです. そして$G$に新しい辺を追加しても連結なままです. 従って「連結性」は monotone increasing です. 他にも「辺を持つ」「直径$\leq 100$である」「辺連結度が100以上である」「ハミルトン閉路を持つ」などの数多くの重要な性質が monotone increasing となります.
一方、性質$\mathcal{P}$を満たすグラフ$G$からどの辺を削除しても依然として$\mathcal{P}$を満たすならば, 性質$\mathcal{P}$は monotone decreasing であるといいます. 例えば「平面的である」「森である」「ハミルトン閉路を持たない」などの性質が monotone decreasingとなります.
$\mathcal{P}$をmonotone increasingであるとします. このとき必ず相転移が発生するような閾値関数が存在するということが証明されています (Bollobas, Thomasson, 1997). 具体的には
nontrivial で monotone increasingな性質 $\mathcal{P}$に対し, ある$p^*=p^*(n)$が存在して
$p=\omega(p^*)$ならばほとんど確実に$G(n,p)$は$\mathcal{P}$を満たし, $p=o(p^*)$ならばほとんど確実に$G(n,p)$は$\mathcal{P}$を満たさない.
ことが示されています(monotone decreasing についても同様のことが成り立ちます). 例えば, 「辺を持つ」という性質では$p^*=n^{-2}$となります.
2.4. 閾値関数上の振る舞い
$p=o(n^{-2})$, $p=\omega(n^{-2})$に対する$G(n,p)$の辺の有無について解析してきました. それではこれらの中間, すなわち $p\sim c\cdot n^{-2}$のときはどうなるでしょうか?
$m$はiidな指示関数の和として書けるので, 二項分布$\mathrm{Bin}\left(\binom{n}{2}, p\right)$に従う確率変数です. ここで, ポアソンの極限定理によると,

となるので (ここでは確率密度関数が各点収束するという意), 今回の場合は
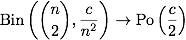
となります. 即ち, 辺の本数$m$は漸近的に平均$c/2$のポアソン分布に従うため, $\mathrm{Pr}(m=0) \to e^{-
様々な性質$\mathcal{P}$について, $p$が閾値関数上のときの$G(n,p)$の振る舞いの確率にはポアソン分布が絡んできていることが分かっています. 例えば$G(n,p)$の頂点を一つ固定してその次数を確率分布 $d$ で表すと, 明らかに $d$ は二項分布 $\mathrm{Bin}(n-1,p) \sim \mathrm{Bin}(n,p)$に従います. 従って
・$p=o(n^{-1})$のときは

・$p=\omega(n^{-1})$のときは, $d$が指示関数の和で表せることを用いると

・$p\sim c\cdot n^{-1}$のときは, ポアソン極限定理より, $d$は漸近的に平均$c$のポアソン分布に従うため,

が簡単に示せます. 特に$d=0$ということは固定した頂点が孤立点であり, つまり$G(n,p)$が非連結であるということになるので,
即ち $p\sim c/n$のときは正の確率で$G(n,p)$は非連結になることが示せました.
実際には頂点を$k$個だけ固定してそれぞれの次数を$d_1,\ldots,d_k$として$k$個の確率変数を定義すると, それぞれは漸近的に平均$c$のポアソン分布に従い, しかも実は漸近的にこれらの確率変数は独立であることが言えます. つまり
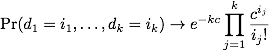
となり, グラフが連結であるならば $d_1>0,\ldots,d_k>0$となるので

今, $k$は任意の自然数だったので, 右辺は任意に小さくできるので,

つまり, $G(n,p)$はほとんど確実に非連結であることが示せました.
3. ランダムグラフ理論の面白い定理
ランダムグラフ理論では閾値関数などの様々な定理が知られているので個人的に面白いと思ったものを列挙します.
3.1. 連結性

とおきます. このとき

3.2. 頂点連結度
グラフ$G$が$k$-connectedであるとは, $G$を非連結にするためには最低でも$k$個の頂点を削除しなければならないことを意味します.

とします. このとき

3.3. ハミルトン閉路
ハミルトン閉路とは, 全ての頂点を一度ずつ通るような閉路のことです. 与えられたグラフがハミルトン閉路を持つかどうかを判定する問題はNP-完全で多項式時間では判定できないとされていますが, ランダムグラフがハミルトン閉路を含むかどうかもまた大きな難問でした.

とします. このとき,

3.4. 最大独立点集合のサイズ
グラフの独立点集合とは, 頂点部分集合$S\subseteq V$で$S$の任意の二頂点間に辺が存在しないようなものです. 独立点集合のうち要素数最大なものを最大独立点集合といい, その要素数を$\alpha(G)$と書きます. 与えられたグラフに対して$\alpha(G)$を計算する問題はNP-困難ですが, ランダムグラフ理論においては次の結果が知られています.
$p\in(0,1)$を定数とし, $b=\frac{1}{1-p}$とします. このときほとんど確実に

つまり, おおよそ $\alpha(G(n,p)) \simeq 2\log_b n$.
3.5. 彩色数
グラフの彩色(頂点彩色)とは, 頂点から色への写像で, 隣接頂点同士は異なる色に写される(塗られる)という性質を持ったものです. 彩色が存在するような色の種類数のうち最小の値を彩色数と呼び, $\chi(G)$で表します. 与えられたグラフ$G$に対して$\chi(G)$を計算する問題はNP-困難です.
$p\in(0,1)$を定数とし, $b=\frac{1}{1-p}$とします. すると
おおよそ $\chi(G(n,p)) \simeq \frac{n}{\log_b n}$ となります.
(注:) 彩色数と最大独立点集合の間には, $\chi(G)\alpha(G)\geq n$という関係があってこれを用いています.
4. おわりに
ランダムグラフ理論の動機を概説し, first order method, second order ethod, Poisson approximation theoremについて紹介しました.
私は東大でランダムグラフ理論について研究していますが, 日本にはランダムグラフをやっている人があまり居ません(少し寂しいことですが...). ランダムグラフ理論で用いられる確率的議論(そしてそのアイデア)は, 乱択アルゴリズムの解析や組合せ論において非常に有用で, それらを学ぶことはランダムグラフのみならず他の分野でも大きな武器になるのではないかと思います(あと二項係数に強くなれます). グラフ理論と確率論のインターセクションにあるランダムグラフ理論はそれらの深い理解に通じる面白い理論であり, そしてランダムグラフ理論の勉強を通じて確率論の深い理解に繋がることがあるので, 本格的に研究しなくても学んでみる価値は大いにあると信じています.
参考文献
[1] R. Diestel, "Graph Theory"
[2] A. Frieze, M. Karoński "Introduction to Random Graphs" (著者がドラフトをウェブ上で公開しています)
[3] Bollobás, "Random Graphs"