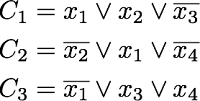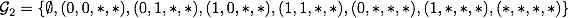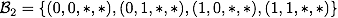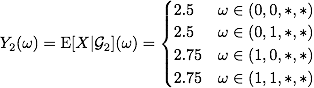グラフが平面的であることの必要十分条件一覧

グラフ$G$を考える.
単射 $\phi:\,V\to\mathbb{R}^2$ 及びジョルダン曲線の族 $(J_e)_{e\in E}$ が存在し, 次の性質を満たすとき, $G$ は平面的であると定義します. 特に$G$が平面的グラフであるとき, 組 $(\phi,(J_e)_{e\in E})$を$G$の埋め込みと呼びます.

性質:
$G$ の各辺 $e=\{u,v\}\in E$に対し,

• $J_e$ は 点 $\phi(u)$ と点 $\phi(v)$ を結ぶ.
• $J_e\backslash \{\phi(u),\,\phi(v)\} \cap \left(\bigcup_{v\in V} \{\phi(v)\} \cup \bigcup_{f \in E\backslash \{e\}} J_f\right)=\emptyset$

$J\subseteq \mathbb{R}^2$ がジョルダン曲線であるとは, 適当な連続な単射 $f:[0,1]\to\mathbb{R}^2$の像として$J$が表せることを指します.

ちなみに, いわゆる「平面グラフ」という言葉は「平面に埋め込まれた」グラフを指すのであって「平面に埋め込める」グラフは指しません.

以下は全て同値です:

• グラフ$G=(V,E)$が平面的である.
• $G$は単純なサイクル基底 (任意の辺$e\in E$に対して$e$を含む閉路が高々2つであるようなサイクル基底)を持つ (MacLaneの定理).
• $K_5$ 及び $K_{3,3}$ をマイナーとして含まない (Wagnerの定理).
• $K_5$ 及び $K_{3,3}$ を位相的マイナーとして含まない (Kuratowskiの定理).
• ある$k\in\mathbb{N}$が存在して, $G$の禁止マイナー $\mathrm{Forb}(G)$ ($G$をマイナーとして含まないような有限グラフの全体)に属する任意のグラフは木幅が高々$k$である (Seymour).
• $G$に対応するグラフ的マトロイド$M$の双対マトロイド$M^{*}$をとったとき, これが別のグラフ$G^{*}$に対応するグラフ的マトロイドとなる (このとき$G^*$は平面的グラフの双対グラフになっている).
• 抽象的双対を持つ.

他にもめっちゃ色々あったはず (学んだら追加していく).

（計算が）ヤバイ級数

は有名です(前者はバーゼル問題で後者は部分分数分解で計算できます)。それでは








はどうなるのでしょうか？？　収束するのは明らかです。計算してみましょう。
（厳密な議論が欠けている箇所が幾つかあるので注意してください）

級数をグッと睨むと、





と変形出来そうな気がします。ここでおもむろにwikipediaを参照すると




と書けるらしいので($B_k$はベルヌーイ数)、元の級数は





となります。ここでおもむろにwikipediaを参照すると、




という双曲線関数の謎テイラー展開（ローラン展開）が得られるので、収束半径を無視して$x=\pi$を代入して整理すると




従って





となります。
（ちなみに数値的にもこの値は合致します)

余談

ゼータ関数は



と書ける（らしい）ので、級数に代入して、総和と積分の交換が出来ると信じて更に収束半径諸々を無視して無理やり計算すると




となります（最後の等式は$\sin$のテイラー展開です)。

従って、(多分)




が成り立ちます（多分）

古典的確率論から測度論的確率論へ (条件付き期待値)

0. 概要

条件付き確率は確率論における重要な概念あり, マルチンゲールを定義するために不可欠です. 従って測度論的確率論を勉強していくと必ずこの概念に出会いますが, その理解は非常に難解(気持ちが分かりにくい)で, 一つの大きな壁であるといえます. 本記事は

• 測度論的確率論を勉強してみたけど条件付き期待値のキモチがいまいち分からない.
• なんとなく言葉は知ってるけどちゃんとした定義はよく知らない.

という人向けに, 直感的な説明とちゃんとした定義を織り交ぜて条件付き期待値について解説します. 本記事は測度論的確率論の基本的な概念を前提知識として仮定します.

本記事では古典的確率論における条件付き期待値から出発して測度論的確率論における条件付き期待値を「導出」していきます. 以前の記事で少しだけ条件付き期待値について書いてあるので, 理解の助けになるかもしれません.

1. 古典的確率論における条件付き期待値

条件付き期待値とは, $\mathrm{E}[X|\mathcal{G}]$で表されるスカラー値です. 古典的確率論においては条件付き確率を定義してから条件付き期待値を定義します. つまり$A,B$をそれぞれ事象として, $\mathrm{Pr}(A|B)=\mathrm{Pr}(A\cap B)/\mathrm{Pr}(B)$と定義した後に, 条件付き期待値を



と定義します. つまり古典的確率論では条件付き期待値は確率変数と事象の組に対してスカラー値を割り当てる関数と見なしていて, $\mathrm{E}[X|B]$は(確率変数, 事象)の組を受け取ってスカラー値を返す関数になるわけです. しかし, 測度論的確率論における条件付き期待値は全然異なっています.

2. 確率変数としての条件付き期待値

測度論的確率論では確率空間を$(\Omega,\mathcal{F},P)$の三つ組として定義し, 事象とは$\mathcal{F}$の元であると考えます. また, 確率変数は$\Omega\to\mathbb{R}$の関数であると考えます. 測度論的確率論ではまず条件付き期待値を定義してから条件付き確率を定義するので, 古典的確率論とは定義の順番が逆になります. そこでまず, 条件付き期待値を定義してみることにします.

$\mathcal{B}=\{B_1,\ldots,B_K\}$を$\Omega$の分割とします. つまり各$B_i\subseteq \Omega$であり, しかも$B_i\cap B_j=\emptyset$ (for $i\neq j$) かつ$\bigcup_{i=1}^K B_i=\Omega$を仮定します. 確率変数$X$と$\Omega$の分割$\mathcal{B}$に対し, 確率変数$Y:\Omega\to\mathbb{R}$を



とします. (Fig.1) ここで$\mathrm{E}[X|B_i]$は(古典的な意味での)条件付き期待値だと思ってください. 結論から言うとこの$Y$が条件付き期待値みたいなものになっていて, 気持ちとしては$Y=\mathrm{E}[X|\mathcal{B}]$になります.

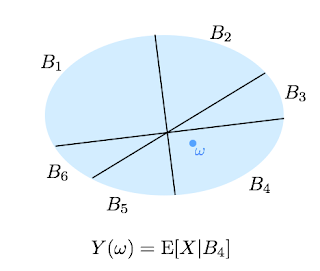FIg.1: $Y$の定義

　イメージとしては, $Y$は確率変数$X$を, 分割$\mathcal{B}$の下で出来るだけ近似しています. $Y$は各分割$B_i$内の二つの要素が区別出来ないという制約の下で出来るだけ$X$っぽい確率変数になっています. なので, より細かい分割に対して同じように$Y$を考えると, 関数としてはより「細かい」ものになっていきます. つまり分割$\mathcal{B}'$を分割$\mathcal{B}$より細かいもの(FIg.2 参照)とすると, $\mathrm{E}[X|\mathcal{B}']$は$\mathrm{E}[X|\mathcal{B}]$よりもより良い近似になっていることが分かります.

Fig.2: $\mathcal{B}$よりも$\mathcal{B}'$の方が細かい分割になっている.

さらに, $Y(\omega)$を$B_i$内で積分すると(直感的な議論だと思って読んでください)

つまり, $\int_{B_i}YdP=\int_{B_i}XdP$ という関係が成り立ちます(この関係が重要です).

3. 測度論的確率論における条件付き期待値の定義

測度論的確率論では事象とは$\sigma$-集合体の要素です. また, 前まではdisjointな事象の集まりを考えていましたが, ここでは部分$\sigma$-集合族について考えます.

確率変数$X$と部分$\sigma$-集合体$\mathcal{G}\subseteq \mathcal{F}$に対して, 条件付き期待値$Y=E[X|\mathcal{G}]$は$\Omega\to\mathbb{R}$は確率変数であり, 以下の条件を満たすものと定義します:

1. $Y$は$\mathcal{G}$-可測 (i.e. 任意の$a\in \mathcal{R}$に対して $\{\omega \in \Omega\,:\,Y(\omega)<a\} \in \mathcal{G}$)
2. 任意の$A\in\mathcal{G}$に対して, $\int_A YdP = \int_A XdP$.

条件2の気持ちは上の式で説明した通りです. 条件1は「近似」の制約の強さを規定しています. つまり「$\mathcal{G}$-可測である」という制約条件の中で$X$を近似したとき, もっともよく近似出来ている確率変数が$Y=\mathrm{E}[X|\mathcal{G}]$であると解釈します. なぜ条件1が制約条件を表すのかについては以前の記事や後に出てくる例を見ると分かり易いと思うので, 後ほど取り上げます.

そもそも本当に条件1,2を満たす$Y$が存在するのかについてですが, ラドン＝ニコディムの定理からalmost everywhereの意味で一意に定まります.

ここではラドン=ニコディムの定理を用いず, 有限加法族$\mathcal{G}$に対して条件付き期待値$Y=\mathrm{E}[X|\mathcal{G}]$をちゃんと構成してみます. すると条件付き期待値について何か掴めるようになると思います. まず有限加法族$\mathcal{G}\subseteq 2^{\Omega}$に対し, 以前の記事で述べた$\Omega$の「都合の良い」分割$\mathcal{B}=\{B_1,\ldots,B_k\}$をとってきます (存在性も証明してあります).
この$\mathcal{B}$に対して1節で考えた$Y$を考えます. すると実は$Y=\mathrm{E}[X|\mathcal{G}]$となることが示せます.

つまり, 有限加法族 $\mathcal{G}$ に対しては条件付き期待値$\mathrm{E}[X|\mathcal{G}]$を1節で説明した方法によって具体的に構成することが出来るようになりました.

また, 条件付き確率$\mathrm{Pr}(A|\mathcal{G})$は, 事象$A$の指示関数$1_A$を用いて



と定義されます.

4. 例 (命題論理式)

SAT(充足可能性判定)問題では命題論理式がCNF形式で与えられます. このとき「充足されるクローズの個数が最大となるような」割り当てを求めるという最大化問題を考えることができます. 例として次の論理式$\phi$を考えます.

また, 各節(clause)$C_j$を



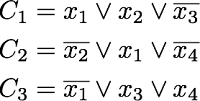
とおきます.

$(x_1,x_2,x_3,x_4)$にそれぞれ等確率に $0$ or $1$ を割り当てると,

$\mathrm{Pr}(C_j$ が充足される$)=1-(0.5)^3$

となり, 確率変数 $X$ を「充足された節の個数」と定義すると, $\mathrm{E}[X]=3-3\cdot (0.5)^3=2.625$ となるはずです. ここで確率空間 $\Omega$ は $\{0,1\}^3$ で, $\sigma$ -集合体 $\mathcal{F}$ は $2^{\Omega}$ とします.

ここで, 4回の(公平なコインによる)コイントスによって$x_1,x_2,x_3,x_4$の割り当てがこの順にランダムに決まっていく過程を考えます.

・$x_1$の値が決定したとき:

$(x_1,x_2,x_3,x_4)$の割り当ては $(x_1,*,*,*)$ となります($*$はランダムビット). 従って事象としては$\{(x_1,r_2,r_3,r_4)\,:\,r_2,r_3,r_4\in \{0,1\}\}\in \mathcal{F}$が発生したことになります. そこでこの事象を含む最小の$\sigma$-集合体 $\mathcal{G}_1$ を考えます. $\mathcal{G}_1$は補集合で閉じていなければならないので

$\mathcal{G}_1=\{ \emptyset, (0,*,*,*), (1,*,*,*), (*,*,*,*)=\Omega \}$

となります. ここで$Y_1=\mathrm{E}[X|\mathcal{G}_1]$を考えましょう. 3節で説明した方法により, 次のように$Y_1$を具体的に構成できます: $\mathcal{G}_1$の「都合の良い」分割として$\mathcal{B}=\{(0,*,*,*),(1,*,*,*)\}$ をとります. これはちゃんと都合の良い分割になっています. ここで$\mathrm{E}[X|(0,*,*,*)],\,\mathrm{E}[X|(1,*,*,*)]$をそれぞれ計算してみます.

・$x_1=0$が定まったとき, 節$C_3$は確率1で充足されるので
$\mathrm{E}[X|(0,*,*,*)]=2-2\cdot (0.5)^2+1=2.5$

・$x_1=1$が定まったとき, 節$C_1,C_2$は確率1で充足されるので
$\mathrm{E}[X|(1,*,*,*)]=2+(1-(0.5)^2)=2.75$

以上より, $Y_1=\mathrm{E}[X|\mathcal{G}_1]$は




となります. 当然のことながら, $\mathrm{E}[Y_1]=0.5\times(2.5+2.75)=2.625=\mathrm{E}[X]$となっています.

・$x_1,x_2$の値が決定したとき:

先ほどと同様の考察を続けます. $\{(x_1,x_2,*,*)\}$を含む最小の$\sigma$-集合体$\mathcal{G}_2$は,



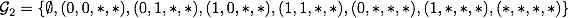
となります ($(0,*,*,*), (1,*,*,*)$が含まれていることに注意). そして分割$\mathcal{B}_2$としては



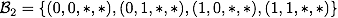
をとれます. (古典的な意味での)条件付き期待値をそれぞれ計算してやると,



となるので,



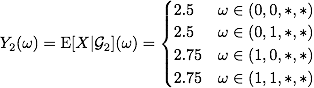
ここで, $\mathcal{G}_2$は$\mathcal{G}_1$よりも「細かい」ものになっていることがわかります. この後コイントスを続けていくとより細かいσ-集合体が得られ, 対応する条件付き期待値もまたより細かい関数になっていくことがわかると思います. そして最終的に4つの変数の割り当てが決定すると$\mathcal{G}_4=\mathcal{F}$となり, $Y_4=X$となります.

このように, 「過程が進んでいくにつれて情報が決定していき, 対応する$\sigma$-加法族が細かくなっていく」ことが重要で, その列$(\mathcal{G}_t)$をフィルトレーションと呼びます.

5. まとめ

古典的確率論における条件付き期待値から出発し, これを測度論的確率論における条件付き期待値の概念に(有限加法族に限定して)拡張していきました.
更に, 命題論理式の例を用いて, 観測される事象に応じて$\sigma$-集合体が細かくなっていき(フィルトレーション), それに応じて条件付き期待値がどんどん近似として精度の良いものになっていくことを見ていきました.

これらの概念はマルチンゲールを学ぶ出発点となるので, よく理解しておくと良いと思います.

有限加法族の分割

有限加法族とは, 有限集合$E$上のσ-加法族 $\mathcal{G}\subseteq 2^E$ でとなるものです. 有限加法族を台集合の分割を用いて表現する定理を証明します.
(おそらく既存の結果として知られているほどの簡単なものですが, そういうのを調べず私が個人的に見つけた証明を載せているので, もし関連結果 or よりスマートな証明をご存知の方がいらしたら教えていただければ幸いです).

この定理を使えば, 有限加法族に対する条件付き期待値を具体的に構成することが出来ます.

(有限でない場合は無理です)

最大平均次数と彩色数について

グラフ$G$に対して



を$G$の最大平均次数 (maximum average degree) と言います.  ここでグラフ$H$に対し$||H||$は$H$の辺数, $|H|$は$H$の頂点数を表します.
頂点$v$に対して$d(v)$で$v$の次数を表すことにすると, 握手補題より$2||H||=\sum_{v\in V(H)} d(v)$となるので, $\frac{2||H||}{|H|}$は$H$の平均次数を表しています. この値はグラフの「疎っぽさ」を表すような値になっていて, 色々と興味深い結果が知られています. 実は最小カットを二分探索の判定として用いることによって多項式時間でこの値を計算することが出来ます.

$\mathrm{mad}(G)$はグラフ理論の有名な本Sparistyにも重要な指標の一つとして紹介されていて, 次のような事実が(証明なしに)紹介されています.

$\chi(G)\leq \lfloor \mathrm{mad}(G) \rfloor+1$.

つまり$\mathrm{mad}(G)$を使って彩色数$\chi(G)$を上から抑えることができます. 非自明な感じがするので今回はこの事実の証明を載せたいと思います. 内容としては$\chi(G)\leq \mathrm{mad}(G) +1$を示しています(床関数をとっても本質的には変わらないので).

(この証明は私が考えたものなので, 他にもっとスマートな証明を知っている方がいらしたら教えていただければ幸いです).







[1] A Fast Parametric Maximum Flow Algorithm and Applications, G. Gallo, M.D. Grigoriadis, R. E. Tarjan (1986)