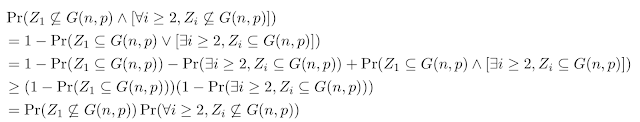color-codingと脱乱択化

乱択アルゴリズムとは, ランダムネスの力を上手く活用したアルゴリズムのことで, ここでは「必ず多項式時間で終わるが間違った解を出力するかもしれない」というタイプのアルゴリズムを考えます（モンテカルロアルゴリズム）.

本記事では, パラメタ化計算量の分野で有名な乱択アルゴリズムとしてcolor coding[4]を紹介し, その「脱乱択化」の方法 (perfect hash family) を紹介します.

1. color coding

1.1. 背景 (k-PATH)

グラフGが与えられたとき, それが長さkのパスを持つかを判定する問題(k-PATH)を考えます. パスは同じ頂点を二度通らないことに注意してください. $k=n-1$ のとき, ハミルトンパスの判定問題を表現するのでこの問題は $k$ を入力としたときはNP完全となります. 一方で $k=O(1)$ としたときは $n^k$ 時間, すなわち多項式時間で解くことが出来ます. それでは, $k=O(\log n)$ の時は多項式時間で解けるでしょうか? $k=\sqrt{n}$ のときはどうでしょうか? 結論から言うと, $k=O(\log n)$ならばk-PATHは多項式時間で解けますが, $k=\omega(\log n)$の場合は(ETHの下で)多項式時間で解けないだろうと予想されています. color codingを使うと, k-PATHを $2^{O(k)}\cdot n^{O(1)}$ 時間で解くことができます. 以下のそのアルゴリズムを紹介していきますが, 同じ内容は吉田 悠一さんによるこちらの記事にも非常に分かりやすく載っているので紹介させていただきます.

1.2. アルゴリズム

1. 与えられたグラフ $G=(V,E)$ の各頂点をランダムに $k+1$ 色で塗ります. つまり, 各頂点に対して$\{1,\ldots,k\}$から一様ランダムに一つの値を選択しその値の色で塗ります.




2. 色付きグラフ $G=(V,E)$ がカラフルな k-path を含むかどうかを判定します. カラフルなk-path とは, 長さkのパスであって各頂点の色が全て異なる (i.e., $k+1$ 種類の色全てを含む) ようなものです. もしカラフルな k-path を含んでいたら, 元のグラフ $G$ は k-path を含むので終了し, そうでなければステップ1に戻ります.

1.3. アルゴリズムの解析

与えられたグラフ $G=(V,E)$ が k-path を含んでいたとして, その頂点を $v_1,\ldots,v_{k+1}$ としましょう. これらの $k+1$ 個の頂点がカラフルになる確率は

$\frac{k!}{k^k} \approx \sqrt{2\pi k} \exp(-k) \leq 3^{-k}$

となります (スターリングの近似を用いました). したがって上述のステップ1-2を $9^k$回繰り返したとき, パス$(v_1,\ldots,v_{k+1})$が毎回カラフルにならない確率は

$(1-3^{-k})^{9^k} \leq \exp(-3^{-k}\cdot 3^{2k}) = \exp(-3^k)$

となり, 非常に小さくなります (ここでは $1+x\leq \mathrm{e}^x$を用いました). つまり非常に高確率で, $9^k=2^{O(k)}$回の繰り返しの中で一回は k-path はカラフルになり, ステップ2で検出されるので高確率でk-PATHを解くことができることになります.

1.4. カラフルなk-パスの検出

動的計画法を使ってカラフルなk-パスの検出を $O(2^k\cdot n^3)$ 時間で解くことが出来ます. 二頂点$u,v\in V$および色の集合$S\subseteq \{1,\ldots,k+1\}$に対して配列として

$\mathrm{T}[u][v][S]:=$頂点$u$から$v$への, $S$-カラフルなパスが存在すればtrue, そうでなければfalse.

と定めます. ここで $S$-カラフルなパスとは, $|S|$個の頂点からなるカラフルなパスで, 各$c\in S$に対して色$c$で塗られた頂点を一個だけ含むようなものです (下図参照).

色つきグラフ$G$において$N(v)$で頂点$v$の隣接点の集合を表し, $\chi(v)\in \{1,\ldots,k+1\}$で$v$の塗られた色を表すこととします.

すると, $\mathrm{T}[u][v][S]$に対して以下の漸化式が成り立ちます.

$\mathrm{T}[u][v][S]=\bigvee_{w\in N(v)}\mathrm{T}[u][w][S-\{\chi(v)\}]$.

basic caseとして $\mathrm{T}[v][v][\{\chi(v)\}]=\mathrm{true}$ と定めます. また, 自明ですが$\{\chi(u),\chi(v)\}\not\subseteq S$ならばT[u][v][S]=falseです. これにより, カラフルk-パスの判定は$O(2^kn^3)$時間で解けるので, アルゴリズム全体では$9^k\cdot n^3=2^{O(n)}\cdot n^{O(1)}$時間で解けます ($n$の右肩の値はおそらく$2$になると思いますが, 大雑把に見積もっても高々$3$なのは明らかなので今回はそう記しました).

1.5. その他の問題への応用

k-PATH以外にもk-CYCLE (長さkの閉路の検出問題) といった問題も color coding を応用したアルゴリズムによって $2^{O(k)}\cdot n^{O(1)}$時間で解くことができます. 一般に, 入力で与えられたグラフ$G$が頂点数$k$の別のグラフ$H$を含むかどうかは 全探索により$O(n^{k+O(1)})$時間で解けますが, color codingを使うと $2^{O(k)}\cdot n^{O(\mathrm{tw})}$ 時間で解くことが出来ます (twは$H$の木幅です). したがってtwが定数ならば$2^{O(k)}\cdot n^{O(1)}$時間で解けます.

1.6. k-PATHに対するより早いアルゴリズム (advanced topic)

P≠NP予想より強いETHという予想を仮定すると, k-PATH問題は$2^{o(k)}\cdot n^{O(1)}$時間では解けないことが知られています[1]. 今回紹介したcolor coding では$9^k\cdot n^3$時間でしたが, 解析をちゃんとやると $O(\mathrm{e}^kn^3\log n)$時間でwith high probability (i.e., 適当な定数$\epsilon>0$に対し確率 $\geq 1-n^{-\epsilon}$) で正解するアルゴリズムになるはずです. では, 例えば$2.3^k\cdot n^{O(1)}$時間で解けるのでしょうか?

結論から言うと, $2^{k}\cdot n^{O(1)}$時間の乱択アルゴリズムが存在します[2]. このアルゴリズムは

1. 「グラフがk-pathを含まない iff Pは恒等的に0」となる多項式Pを構成する (但しガロア体$\mathrm{GF}(2^{\lceil 4k \rceil})$上の多項式).

2. Schwartz-Zippelの補題を用いてPが恒等的に0かどうかを乱択で判定する (その際に包除原理を用いる).

という流れです. Schwartz-Zippelの補題については相馬 輔 さんによる こちらのページで証明も含めて紹介されています. 更に, 現在では$2^{0.75k}\cdot n^{O(1)}$ 時間アルゴリズムも知られています[3].

この$2^{k}\cdot n^{O(1)}$時間アルゴリズムは様々な道具が登場し非常に面白いものなので, 機会があれば紹介したいと思います.

2. 脱乱択化 (derandomization)

脱乱択化とは文字通り「ランダムネスを排除する」ことです. これまで考えていたアルゴリズムは高確率で正解を計算するものでしたが, 脱乱択化をすると必ず正解を計算するアルゴリズムになります. 計算量理論では, 多項式時間の乱択モンテカルロアルゴリズムで(高確率で)解ける問題のクラス (BPP) が多項式時間で決定的に解ける問題のクラス(P) と等しいかどうかは未解決ですが, 多くの研究者はP=BPPだと信じているようです. P=BPPならば多項式時間乱択アルゴリズムは多項式時間のまま脱乱択化できる, ということになります. ここでは, それに関連したポジティブな結果の一つとして, 先ほど紹介したcolor codingの脱乱択化の方法について紹介します. キーワードはperfect hash familyです.

2.1. color coding is revisited

color codingに基づくアルゴリズムは

(i) グラフを$k$色で塗る.

(ii) カラフルな部分グラフを動的計画法で$2^{O(k)}\cdot n^{O(1)}$時間で見つける.

(iii) 見つけたい部分グラフが(i)でカラフルになる確率が$\geq 2^{-O(k)}$となるので, $2^{O(k)}$回(i)と(ii)を繰り返す.

というものでした.

即ち, 「見つけたい部分グラフが(i)でカラフルになるような塗り分け」をランダムネスを使わず決定的な方法で見つけられたら脱乱択化になります. 

2.2. Perfect hash family

入力で与えられるグラフを$G=(V,E)$とし, その頂点数を$n=|V|$とします. そして塗り分けの集合 $\mathcal{F}$ を考えます. $[m]:=\{1,\ldots,m\}$と表すことにすると, 各要素 $f\in \mathcal{F}$は写像$f:[n]\to [k]$となり, $f(v)$は頂点$v$の色を意味します. つまり$\mathcal{F}$は写像の集合になります. 

定義.

$\mathcal{F}$ が以下の条件(＊)を満たすとき, $\mathcal{F}$は $(n,k)$-perfect hash familyと呼びます.

(＊) サイズ$k$の任意の部分集合$S\subseteq [n]$ of $|S|=k$ に対して, ある$f\in\mathcal{F}$が存在して, $f(S)=[k]$となる (i.e., 塗り分け$f$の下では$S$はカラフルになる).

$\mathcal{F}$ を $(n,k)$-perfect hash family としましょう. グラフ$G=(V,E)$が入力で与えられたとき, $\mathcal{F}$を構成して全ての$f\in \mathcal{F}$のそれぞれに対してcolor codingの動的計画法のアルゴリズムを使ってカラフルな部分グラフを判定すれば, $T(n,k)+|\mathcal{F}|\cdot 2^{O(k)}\cdot n^{O(1)}$時間で決定的に解くことが出来ます. ここで$T(n,k)$は$\mathcal{F}$の構成にかかる時間です.

$(n,k)$-perfect hash familyについては以下の結果が知られています[4]:

定理.

$(n,k)$-perfect hash family $\mathcal{F}$で

$|\mathcal{F}|\leq \mathrm{e}^kk^{O(\log k)}\log n$

を満たすものを $\mathrm{e}^kk^{O(\log k)}n\log n$ 時間で構成することができる.

これにより, color codingの脱乱択化を$O(\log n)$時間程度のロスでやることが出来ます.

参考文献

[1] D. Lokshtanov, D. Marx, and S. Saurabh. Lower bounds based on the Exponential Time Hypothesis. Bulletin of the EATCS, 84, pp.41–71, 2011.

こちらのサーベイ論文は(題目通り)ETHやSETHの基づいたlower boundとその証明テクニックを幅広く紹介しており, 大変良い論文です. SETHについては以前の記事で紹介しています.

[2] R. Williams, Finding a path of length $k$ in $O^*(2^k)$ time, Journal Information Processing Letters, 109-6, pp. 315-318, 2009.

color codingではk-PATHを$\mathrm{e}^k n^{O(1)}$時間でしたが, こちらの論文はSchwartz-Zippelの補題を用いて$O(2^{k}n^{O(1)})$時間でk-PATHを解くアルゴリズムを提案しています.

[3] M. Cygan, F. V. Fomin, L. Kowalik, D. Lokshtanov, D. Marx, M. Pilipczuk, M. Pilipczuk S. Saurabh, Parameterized Algorithms, Springer International Publishing, 2015.

パラメタ化計算量に関するアルゴリズムを幅広く紹介しています. FPTといった計算量クラス基本的な定義やW-階層といった困難性のクラスやそれらに基づくlower boundについても載っています. 各chapterの後ろには豊富な演習問題とBibliographic notesが載っており, ここには計算量の改善の歴史などが載っています. 誤植もあまりなく, 英語も読みやすいため個人的には非常にオススメの本です.

[4] N. Alon, R. Yuster, U. Zwick, Color-coding, J. ACM, 42-4, pp. 844-856, 1995.

color codingを提案した非常に有名な論文です. 論文中では$k$-CYCLE (長さ$k$の閉路の検出) を用いてcolor codingのアルゴリズムを説明していますが, それのみならず, 木幅が定数のグラフの検出, perfect hash familyを用いた脱乱択化についても書かれています.

FKG不等式とその解釈

FKG不等式という不等式を紹介します.

私自身そこまで詳しくはなく, 考えていたら面白い解釈を思いついたので記事に起こした次第です.

形がシンプルで, よく考えると劣モジュラ性に現れる限界効用逓減性っぽい雰囲気が感じられ, さらに名前がカッコイイので個人的に激アツな不等式です.

準備

・$\{0,1\}^m$上の離散確率を考える (例えばErdős–Rényi model).

・$f,g:\{0,1\}^m \to \mathbb{R}_{\geq 0}$ ... monotone increasing ($\{0,1\}^m$上の順序はbitwiseで比較)

・各$i=1,\ldots,m$に対してbinaryな確率変数$X_i$を定め, $\Pr(X_i=1)=p_i$とする.

・このとき, $f(X_1,\ldots,X_m)$ と $g(X_1,\ldots,X_m)$ は確率変数となる. 

定理 (FKG不等式)

$\mathrm{E}[fg]\geq \mathrm{E}[f]\mathrm{E}[g]$.

実は$\{0,1\}^m$は束にまで一般化できる. 

Remark.

・$f,g$がどちらも monotone decreasing でも成り立ちます (両辺に $-f,-g$ を代入).

・要するに共分散 $\mathrm{Cov}[fg]\geq 0$ と言っているだけなので, 両方ともmonotone ならば正の相関がある, みたいな認識です.

例 (Erdős–Rényi modelの部分グラフ)

$f,g$としてindicator functionを考えるのが一番簡単でしょう.

$m=\binom{n}{2}$, $p_i=p\in[0,1]$とすると, この設定はErdős–Rényi model $G(n,p)$と同等になる. その頂点集合を$V=[n]=\{1,\ldots,n\}$と定め, $Z_1,\ldots,Z_k\subseteq E(K_n)$を$V$上の完全グラフ$K_n$の辺部分集合とする.

例えば, 二頂点$s,t\in V$を固定し$Z_1,\ldots,Z_k$を$st$を結ぶ長さ4のパスの全体を考えたりできます. ここで各$Z_i$は頂点にラベルがついていることに注意してください. 従ってこの例だと$k=(n-2)(n-3)(n-4)$となります.

ここで確率

$\Pr(\forall i,Z_i\not\subseteq G(n,p))$

を考えます. FKG不等式を用いると

$\Pr(\forall i,Z_i\not\subseteq G(n,p))\geq \prod_i \Pr(Z_i\not\subseteq G(n,p))$

が簡単に示せます (実は使わなくても簡単に示せますが...). それを確認してみましょう.

もし,

が成り立つとしましょう (この部分をFKG不等式を使って示します).

すると

となり, 帰納的に

となります. 最後に成り立つと仮定した部分ですが,

とおくと, monotone increasing (言い換えれば$f(G+e)\geq f(G)$ for any $e\in \binom{V}{2}\setminus E(G)$) なので, FKG不等式より

$\mathrm{E}[fg]\geq \mathrm{E}[f]\mathrm{E}[g]$.

上式にある$\mathrm{E}(\cdot)$はそれぞれindicatorの期待値なので対応する確率となる (証明終).

限界効用逓減性

上の例では$f,g$を事象のindicatorとしていました. それに倣い, $f,g$をそれぞれ事象$A,B$のindicatorとしましょう. FKG不等式より

$\Pr(A\cap B)=\mathrm{E}[fg]\geq \mathrm{E}[f]\mathrm{E}[g]=\Pr(A)\Pr(B)$.

言い換えれば $\Pr(A|B)\geq \Pr(A)$ となります. これを情報量の言葉で書き換えると

$-\log \Pr(A|B) \leq -\log \Pr(A)$ です. つまり「Bの発生を知った上でのA発生の情報量」は「A発生の情報量」より少ないことを意味します. 解釈として, 例えば「食べログで高評価(=Bで条件付けられている)の店Sに入って美味しいものを食べたときの感動(=Aの情報量)」は「なんとなく入った店Sで美味しいものを食べたときの感動」よりも相対的に小さいという感じです.

もちろんこの解釈は$f,g$をindicatorに限った時の話であって, FKG不等式はこれをより一般に単調関数について拡大した不等式である, という見方ができるんじゃないかと思います.

FKG不等式の応用先

- Jansonの不等式の証明

- 本記事で証明したrandom graphのsubgraphの話

- 乱択アルゴリズムの解析 (PPSZ algorithmなど)

など

ランダムグラフの直径の直感的な話

普段はそこそこ真面目な記事を頑張って書いていますが今回はしょうもない話をします. いろんな数学の定理を理解するためにはやはり直感的な理解というのも重要だと思っていて, 今回はランダムグラフの直径についての直感的な理解の助けになるような話を電車で思いついたのでそれを垂れ流そうと思っています. ランダムグラフについては昔の記事にさわりだけ書いてあるので興味のある方はぜひ.

グラフ$G$の直径が $D$ 以下であるということは, どの頂点ペアに対しても長さ$\leq D$のパスが存在するということになります.

今, 各辺が独立に確率$p$で結ばれたランダムグラフ $G(n,p)$ を考えます. このグラフが長さ $l$ のパスを何本持つかを考えてみましょう. 簡単のため $l\in\mathbb{N}$ は定数とします. 期待値的には, 長さ$l$のパスは$l+1$個の頂点と$l$本の辺を持つため, $n(n-1)\cdots (n-l)p^l\approx n(np)^l$だけ含まれています.

ということは長さ$\leq D$のパスは期待値的には全部で $n\sum_{l=1}^D (np)^l \approx n^{D+1}p^D$ だけ含まれています. 冷静に考えると, パスの本数といった「〜の数」というものは指示関数の和によって表すことができます. 今回の場合は$\sum_{P:path}1_{[P\subseteq G(n,p)]}$といった具合です. それぞれの指示関数は独立のいうわけではありませんが, パスが辺素なら独立なので, 「なんとなく独立っぽい感じ」の確率変数の和ということになります. たくさんの独立な確率変数の和は期待値の周りに集中する(c.f. Chernoff bound)ので, $G(n,p)$は長さ$\leq D$のパスを$n^{D+1}p^D$本くらい含んでいそうです. 実際この直感はそこそこ正しくて, Jansonの不等式やこの結果を用いるとChernoffに近い感じの集中性が示せます (ただしどれくらい集中性が強いのかはかなり難しい問題です).

さて, $G(n,p)$の直径が$\leq D$である確率を考えます. 先ほどの直感を信じて長さ$\leq D$のパスが $n^{D+1}p^D$本あるとしましょう. 各頂点ペアにこれらのパスをランダムに「配分」することを考えます. ランダムグラフなのでパスの本数に偏り（例えば頂点1,2間には長さ$D$のパスが114514本あって頂点3,4間には1本もない）みたいなものは起こりにくいはずです。そこで$\binom{n}{2}$個の空のバケツがあってそこに$n^{-1}(np)^D$個のボールを一個ずつランダムに投げ入れたときに, 全部のバケツに少なくとも一個のボールが入っている確率を考えます (このイメージは全ての頂点のペアに長さ$\leq D$のパスが少なくとも一本ある = 直径$\leq D$に対応します). するとクーポンコレクター問題を思い出してもらうと, $n^{D+1}p^D \gg \binom{n}{2}\log \binom{n}{2}\approx n^2\log n$ ならば直径$\leq D$になるような気がします.

まとめると, $n^{D-1}p^D\gg \log n$ならば$G(n,p)$の直径は$D$以下, $n^{D-1}p^D \ll \log n$ならば直径は$D+1$以上となる, ことがなんとなくわかります.


実はこの結果は理論的にも正しいです. また, 「$\gg$」と「$\ll$」の境目に関しては次の結果が知られています.

Thm [p.112, Intruduction to Random Graphsより]
定数$D,c$に対して, $p^Dn^{D-1}=\log (n^2/c)$ を満たすよう$p=p(n)$を定めると, 以下が成り立つ:

• $\lim_{n\to\infty} \Pr(\mathrm{diam}(G(n,p))=D)=\exp(-c/2)$,
• $\lim_{n\to\infty} \Pr(\mathrm{diam}(G(n,p))=D+1)=1-\exp(-c/2)$.

証明はこの記事で説明した話とは全く違いますが, それほど難しくはないです. 距離$D$のペアの個数についてPoisson approximation theoremを適用するために頑張って計算するというものです.

Hardness in P (SETH編)

- Introduction

計算複雑性理論では1950年代以降, 「多項式時間で解けるか否か」の解明が一つのテーマとなっています. しかしそもそも多項式時間で解けることが示されている問題はほとんどなく, 実際にはP≠NP予想を仮定して色々示すということがなされています.

P≠NP予想は「論理式の充足可能性(SAT)と呼ばれる問題を解く決定性チューリング機械上で実行される多項式時間アルゴリズムは存在しない」という予想ですが, よく知られる通りこの予想を仮定すると巡回セールスマン問題だとかグラフの最大クリークといった問題が多項式時間で解くことが出来ないということが導出できます.

一方で (P≠NPの下で) 多項式時間で出来ないからといってそこで研究が終わるわけではありません. 例えばグラフの最大独立点集合を求める問題はNP-困難ですが$O(1.2278^n)$ 時間で解くことが出来ますし, ハミルトン閉路の検出は$O(1.63^n)$時間のモンテカルロ乱択アルゴリズムが知られています. つまり「多項式時間で（多分）解けない」から発展し「具体的にはどれくらいの時間で解けるのか」というトピックの研究が近年盛んに行われており, fine-grained complexityなどと呼ばれています. fine-grainedとは「細かな」というような意味合いです.

もちろん, NP-困難な問題に対する

・近似アルゴリズムやその限界. 例えばPCP定理、Unique games conjectureなど.

・特殊なタイプのグラフに対する高速なアルゴリズム. 例えばFPT (fixed parameter tractability)アルゴリズムやW-階層.

といった方向性の研究も盛んです.

また一方で多項式時間で解けるからといってそこでも研究が終わるわけではありません. 多項式時間で解ける問題をより高速に解こうとする方向性の研究もまた盛んに行われています. 最たる例は行列積で, 素朴に計算すると$O(n^3)$時間かかりますが2018年7月現在最速のアルゴリズムは$O(n^{2.3728639})$時間 [François 2014] です (ちなみにそれ以前の最速アルゴリズムは$O(n^{2.3728642})$時間 [Vassilevska Williams 2011] なのでかなり接戦です). 計算モデルによって計算時間が変わってきますが, 本記事では計算モデルとして$O(\log n)$ bit word RAM モデルを考えます.

今回紹介するのは多項式時間で解ける問題（クラスP）における困難性を追求する研究で,「Hardness in P」と言います. たまに「fine-grained complexity」とも言ったりしますが, クラスPの問題を扱うときはHardness in Pと言うような気がします (厳密に言うとクラスPは判定問題のクラスですが「Hardness in P」という名称はその点には少し目を瞑っているような気がしますし特に混乱も起きないと思うので本記事もそれに倣います). 冒頭で述べたように, 時間計算量の下界を示すようなテクニックはほぼ知られていないため, P≠NP予想といった何かしらの予想を仮定してその下で様々な問題の計算量の下界を導出するといった流れをHardness in Pでもとっています.

ではHardness in Pではどのような予想を仮定するのでしょうか. 結論から言うとたくさんあり, 主にAPSP予想, 3SUM予想, SETHの三つが仮定されることが多いのですが(下図), 本記事ではSETHに焦点を絞って紹介していきたいと思います (APSP予想は以前の記事でちらっと触れています).

- SETH (Strong Exponential Time Hypothesis)

SETHは日本語では強指数時間仮説と呼ばれているそうです. HypothesisとついていますがConjectureだと捉えた方が理解しやすいと考えているので「予想」として扱います（なんでHypothesisなのかはよく分かりません. 信じるか信じないかで使い分けているのでしょうかね). 簡単に言うとSETHは「SATは$O((2-\epsilon)^n)$時間で解けない」という予想です. k-SATはそれぞれの節が高々k個のリテラルからなるCNFで記述された論理式の充足可能性を判定する問題です. 変数の個数を$n$、節の個数を$m$で表します。節の組み合わせから, $m\leq O((2n)^k)$が言えます. 2-SATは多項式時間で解けますが3-SATはNP-完全であることが知られており, 素朴に解くと$O(2^n\cdot m)$時間かかります. 実は3-SATは$O(1.308^n)$時間乱択アルゴリズムが知られており[Hertli, 2014], 決定性アルゴリズムに限るとk-SATは$2^{\left(1-\frac{1.44}{k}\right)n}$時間で解けることが知られています [Moser and Scheder, 2011]. つまり$k\to\infty$とするとその計算時間は漸近的に$2^n$となるわけです. これが$1.99^n$に改善できない, がSETHの主張です。

予想 (SETH) [Impagliazzo, Paturi and Zane, 2001]

任意の$\epsilon>0$に対してある$k>0$が存在してk-SATは$O((2-\epsilon)^n)$時間で解けない.

細かい話をするとこれは「アルゴリズムの列」が存在しないと言っています. SETHの否定は「アルゴリズム列$(\mathcal{A}_k)_{k\in\mathbb{N}}$が存在して各$\mathcal{A}_k$はk-SATを$O((2-\epsilon)^n)$時間で解く, というような$\epsilon>0$が存在する」となります. 自分は以前, SETHをパラメタ化計算量の文脈で解釈しようとし「$k$でパラメタライズされたときにk-SATは$f(k)\cdot (2-\epsilon)^n$時間で解くようなアルゴリズムは存在しない」と誤解していたのですが, これはSETHよりも弱い命題（これはSETHから導出できる)です. またこの二つの主張が等価かどうかもわかっていないと認識しています.

SETHを仮定するとOrthogonal Vectors Conjecture (OVC)と呼ばれる予想が導出され, 実はOVCがHardness in Pにおいて起点となる予想として頻繁に用いられます (ですがSETHの方が著名なので論文のタイトルにはOVCではなくSETHが用いられることが多いような気がします).

- Orthogonal Vectors Conjecture

OVCは強いて和訳するなら「直交ベクトル予想」でしょうか. 次の判定問題を考えます.

問題 (Orhogonal Vectors, 直交ベクトル検出問題)

入力：$A,B$: それぞれ$d$次元$01$ベクトルの集合で$|A|=|B|=n$.

出力：ある$a\in A,\,b\in B$が存在して$\sum_{i=1}^d a_ib_i=0$ならばYes. そうでないならばNo.

Orthogonal Vectorsに対応する和訳が (私の知る限り) ないので, 直交ベクトル検出問題と便宜上呼ぶことにします. この問題は素朴に解くと$O(dn^2)$時間かかりますが, 実は$O(n^{2-1/O(\log(d/\log n))})$時間で解くことが出来ます [Abboud, Williams, and Yu 2015]. $d=k\log n$とするとこれは$O(n^{2-1/O(\log(k))})$時間なので, $k\to\infty$とすると漸近的に$O(n^2)$時間となります. これが$O(n^{2-\epsilon})$時間に改善出来ないというのがOrthogonal Vectors Conjecture (OVC)です.

予想 (OVC)

任意の$\epsilon>0$に対してある$k>0$が存在して$d=k\log n$に対する直交ベクトル検出問題は$O(n^{2-\epsilon})$時間で解けない. つまり、$d=\omega(\log n)$ならばOrthogonal Vectorsは$\Omega(n^{2-o(1)})$時間を要する.

繰り返しになりますが, 計算モデルは$O(\log n)$ bit word RAM モデルです. また, SETHの箇所で説明したようにこの予想でも「アルゴリズム列」の存在性を否定しています.

次の定理が知られています.

定理1 [Williams, 2005]

SETHを仮定するとOVCは真. 対偶をとると, 次元$d=k\log n$の直交ベクトル検出問題を$O(n^{2-\epsilon})$時間で解くアルゴリズム列$(\mathcal{A}_k)$が存在するならば, k-SATは$O((2-\epsilon')^n)$時間で解ける ($\epsilon'>0$は$\epsilon$に依存する定数).

定理1は Sparsification lemma+賢い帰着 によって示すことができます。

定理2 (Sparsification lemma) [Impagliazzo, Paturi and Zane, 2001]

$n$変数$m$節を持つk-SATのインスタンス$\phi$が与えられたとき, 以下の条件を満たすような論理式の集合$\phi_1,\ldots,\phi_l$を出力する$O(2^{\epsilon n})$時間アルゴリズムが存在する ($\epsilon>0$は任意の定数).

1. 各$\phi_i$は$n$変数のk-SATで, 節数は高々$K_\epsilon n$となる ($K_\epsilon$は定数).
2. $\phi$が充足可能 iff ある$i$が存在して$\phi_i$は充足可能.
3. $l\leq 2^{\epsilon n}$.

Sparsification lemmaを用いるとSETHを考える上ではk-SATのインスタンス$\phi$の節数$m$は$O(n)$であるとして良いことになります. Spaisification lemmaがどのようにして定理1の証明に用いられるかを説明しましょう.

定理1において, Orthogonal Vectorsが$O(n^{2-\epsilon})$時間で解けたと仮定し, 何らかの$\epsilon'>0$に対しk-SATを$O((2-\epsilon')^n)$時間で解くことを目標としましょう. 適当に$\delta=\delta(\epsilon)>0$を$\epsilon$に依存するものすごく小さい定数と設定します (後で定められます). k-SATのインスタンス$\phi$をSparsification lemmaによって$\phi_1,\ldots,\phi_l$に分解し ($l\leq 2^{\delta n}$), 各$\phi_i$を解くことを考えます. それぞれの$\phi_i$は高々$K_\delta n$個の節を持っています.

図1: 節数$m=O(n)$なるk-SATを直交ベクトル検出問題に帰着している.

ここで$n$個ある変数を半分ずつ二つのグループに分け, それぞれのグループについて$2^{n/2}$通りの（部分）割り当てを列挙します. 列挙された部分割り当て一つ一つが$d=m\leq K_\delta n$次元ベクトル$\in\{0,1\}^m$をなし直交ベクトル検出問題のインススタンスを形成します. 節$i$が部分割り当てによってtrueになるならば, その節に対応する成分が1にします (図1参照). それぞれのグループに対してこの手続きによってベクトルの集合を生成し, それら二つの集合を$A,B$として直交ベクトル検出問題のインスタンスとします. すると, このインスタンスがYesインスタンス(i.e., 直交ベクトルを持つ)であることと論理式$\phi_i$が充足可能であることが同値であることが簡単に分かります. これは各節はリテラルのorによって結合されたものであるため, 節iが充足されていることと対応する二つの部分割当の少なくとも一方が節iを充足する(i.e., ベクトルの第i成分=0)が等価になるからです. さて, $N=|A|=2^{n/2}$とおきます. ベクトルの次元は$m\leq K_\delta n=O(\log N)$となります. 最初の仮定よりこのインスタンスは$O(N^{2-\epsilon})=O(2^{(1-\epsilon/2)n})$時間で解けます. したがって全体の計算量は

$O(2^{\delta n}\cdot 2^{(1-\epsilon/2)n})=2^{(1-\epsilon/2+\delta)n}$

となり, 適切に$\delta>0$を設定してやると所望の結果が示せます. Sparsification lemmaは節の個数が変数の個数$n$に対して線形にできるという部分が強力ですし, SETHがETHを導出するという命題の証明にも使われます. ちなみにSparsification lemmaの証明には組合せ論におけるsunflower lemmaという命題を用いていて、例えばこちらに分かりやすく載っていますが, 個人的には結構面白いと思います.

ここからはOVCの下で様々な問題の計算量下界を見ていきます.

- 直径 2 vs. 3

直径$3$以下であることが約束されたグラフ$G=(V,E)$が与えられたときにその直径が2か3かを判定する問題を考えます. 直径とは最長の最短経路長として定義され, ここでは辺重みは全て1とします. グラフの頂点数を$n$, 辺数を$m$としたときに（OVCの下で）この判定問題が$O(m^{2-\epsilon})$時間で解けないことが知られています [Roditty and Vassilevska Williams, 2013]. 特にこの結果はグラフの直径の$1.499$-近似が$O(m^{1.999})$時間で計算できないことを意味します.

定理3 [Roditty and Vassilevska Williams, 2013]
与えられたグラフの直径が2か3かどうかを$O(m^{2-\epsilon})$時間で判定出来るならば, OVCは偽である.

注意されたいのは, この定理は密なグラフの直径の計算量については何も言っていません. 実際, 以前の記事で紹介したようにどんなグラフでもその直径は$O(n^\omega \log n)=O(n^{2.373})$時間で計算することが出来るからです.
これを証明したいと思います. 直交ベクトル探索のインスタンス$(A,B)$から次の性質を満たすグラフ$G$を構成することを考えます.

性質: $(A,B)$がYesインスタンスであるならば$G$の直径は3, そうでなければ$G$の直径は2.

図2: ベクトル$a\in A,\,b\in B$が直交するならば$a,b$間の最短経路長は3.

図2のようなグラフ$G$を構成します. $G$の頂点集合は$A,B,[d]=\{1,\ldots,d\},u,v$からなり, ベクトル$a$の第$i$成分が1ならば辺$\{a,i\}$を貼り, $B$についても同様に辺を貼ります. $[d]\cup\{u,v\}$の部分は全頂点ペアに辺を貼ってクリークにし, $A$-$u$間と$B$-$v$間も同様に全ペアに辺を貼ります. すると$G$の直径3以上であることと$(A,B)$が直交ベクトルを持つことが同値であることが分かります (直交していなければ, $\{a,i\},\{b,i\}\in E(G)$なるインデックス$i$が存在して距離2になる).

直径2と3の区別が$O(m^{2-\epsilon})$時間で出来るとしましょう. 直交ベクトル検出問題のインスタンス$(A,B)$から上のようにしてグラフ$G$を構成します (これは$O(nd)$時間でできます). このとき$m=O(nd)=O(n\log n)$なので, $O(m^{2-\epsilon})=O(n^{2-\epsilon+o(1)})$時間で直交ベクトル検出問題が解けることになり, これはOVCに矛盾します.

また, 図2のグラフの木幅は$d+2=O(\log n)$であることに注目すると, 次の結果も示されたことになります.

定理4 [Abboud, Vassilevska Williams and Wang, 2016]
木幅$k$のグラフの直径の$1.499$近似を $2^{o(k)}\cdot n^{2-\epsilon}$時間で計算できるならば, OVCは偽.

証明: $2^{o(k)}n^{2-\epsilon}=n^{2-\epsilon+o(1)}$より明らか.

ちなみに木幅$k$のグラフの直径は(辺に重みがあっても)$2^{O(k\log k)}n^{1+o(1)}$時間で計算できることが[Abboud, Vassilevska Williams and Wang, 2016]において知られており, $2^{O(k)}n^{2-\epsilon}$時間で出来るか否かはこの2年間未解決でしたが, 今年解決されました (この論文は2018年8月開催予定のIPECという国際会議に採択されています. arXivを読む限り, 内容は正しそうだと私は思っています).

- その他の問題

直径の他にも様々な問題に対してSETHの下での時間計算量下界が示されています. 例を挙げると

• 疎グラフの平均距離 (平均距離が計算できれば直径2と3を区別できる).
• 長さ$n$の二つの文字列の編集距離は$\Omega(n^{2-o(1)})$時間かかる [Backurs, Indyk, 2014], 最長共通部分列(LCS)も$\Omega(n^{2-o(1)})$時間かかる [Bringmann, Künnemann, 2015], [Abboud, Backurs, Vassilevska Williams, 2015].
• 直径5と直径8の区別は$\Omega(n^{1.5-o(1)})$時間かかる [Backurs, Roditty, Segal, Vassilevska Williams, Wein, 2018].

などがあります.

- そもそもSETHは正しいのか？

強い予想を仮定すると色々と面白いことが言えるというのはそもそも当たり前です. そもそも第一にそもそも仮定する予想が本当に正しいのかどうかに関しては議論の余地が大いにあります. 例えば行列積は昔は$O(n^{2.999})$時間で解けないと思われていましたが, 実際は (環上で) $O(n^{2.373})$時間で計算できます. しかしSETHが偽ならば回路計算量で強い下界が成り立つという結果も知られています [Williams, 2013]. もちろん, 仮定している予想が本当に正しいかどうかという問題意識はfine-grained complexityをやっている研究者にもありますし, もっと弱い仮定の下でいろんなことを導出するような論文もあります. 

また, 予想がたくさん出てきている, 悪く言えば乱立しているのも実情です. パッと思い浮かぶだけでも

- SETH

- APSP予想 (APSP: All-Pairs Shortest Paths)

- 3SUM予想

- Gap-ETH

- Clique conjecture (サイズ$k$のクリークが$O(n^{k\omega/3-\epsilon})$時間で検出できないという予想. $\omega<2.373$は行列積の指数)

などがあり, ここ1,2年のSODA論文でもこのような予想の下での困難性の結果に関する論文がたくさん出てきています. しかも, 上に挙げた予想に対し「予想Aを仮定すると予想Bは真である」といった結果は一切知られていません.

そもそも計算複雑性理論においては仮定なしで下界を示すような結果は本当に少なく, average case complexityの分野におけるplanted clique conjecture, 近似アルゴリズムにおけるunique games conjectureといった全く上記とは別の予想の下での困難性の結果がたくさん研究されているので, fine-grained complexityだけの問題点ではなく, 今に始まった議論ではありません. しかしSETHが真だとしても偽だとしても様々な計算量下界が導出されるので, とても面白いと思います.